Означення 1. Сукупність чисел кожне з яких є функцією від натурального аргумента, які розміщенні в порядку зростання номерів назив. числовою послідовністю.
Означення 2. Стале число 
називається границею послідовності 
якщо для будь-якого додатного числа 
можна вказати таке натуральне число N, починаючи з якого всі наступні члени послідовності задовольняють нерівність 
(n>N). Записують це так: 
.
Теорема 1. В будь-якій обмеженої послідовності можна виділити збіжну підпослідовність.
Доведення. Нехай послідовність обмежена, тобто 
n є N. Поділимо відрізок 
на дві рівні частини. Оскільки кільк членів нескінченна, в одній із половин міститься нескінченність. Позначимо половину через 
ділимо відрізок пополам, беремо ту частину в якій є нескінченна кільк. елементів і позначимо цей відрізок 
,…. 
,… 
… 
Теорема 2. Для того, що послідовність була збіжна необхідно і достатньо щоб для 
, що n>N, p>0(p є N), слідує нерівність 
Доведення: Для того, щоб послідовність була збіжна, то 
, виконується 
n>N, p>0 (p є N) 
з а слідує 
n>N, p>0 (p є N) 
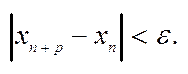
Нехай 
, 
що n>N, p>0 (p є N) 
.
для будь- яких n>N, p>0.
Достатність. Нехай виконується умова:
Розширимо ці границі, щоб охопити перший N, ця послідовність буде обмеженою 
n є N. За попередньою теоремою отримаємо 
Т.доведено.
Теорема 2. Якщо послідовність збіжна, то вона має лише одну границю.
Теорема 3. Будь – яка обмежена монотонна послідовність збіжна.
Теорема 4. Якщо послідовність збіжна, то вона обмежена
Якщо 
, то послідовність (
) називається нескінченно малою. Прикладом такої послідовності є 
Послідовність 
називається неспадною, якщо для всіх її членів виконується нерівність 
, n є N, і зростаючою, якщо для всіх її членів виконується нерівність 
, n є N. Послідовність () називається незростаючою, якщо для всіх її членів виконується нерівність 
, n є N, і спадною, якщо для всіх її членів виконується нерівність 
, n є N. Незростаючі, неспадні, зростаючі і спадні послідовності називаються монотонними послідовностями.
Теорема 1-2. Всяка монотонна зростаюча (спадна) обмежена зверху (знизу) має скінчену границю.
Доведення. Доведемо для випадку монотонно зростаючої і обмеженої числової послідовності. 
n є N. Оскільки послідовність обмежена зверху, то згідно теореми про існування точної верхньої межі і для послідовності 
існує точна верхня границя, тобто 
За Влас. точної верхньої межі 
. По друге: 
знайдемо таке значення 
, таке, що 
В силу монотонності зростання числової послідовності 
матимемо, що для будь-якого слідує 
. Аналогічно для випадку спадної послідовності обмеженої зверху.
Основна формула для числа е: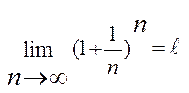 
(1). З рівності (1) випливає інша рівність (
) 
. Доведемо, що 
Нехай х- пробігає, яку-небудь послідовність 
, 
, 
. Звідси 
. Візьмемо від цього ліву і праву границі, які будуть дорівнювати е. Аналогічно і для 
. 
- натуральні логарифми. 
, М= 
