Лінійне програмування – наука про методи дослідження і знаходження екстремальних (найбільших і найменших) значень лінійної функції, на невідомі якої накладаються лінійні обмеження.
Ця лінійна функція називається цільовою, а обмеження які математично записуються у вигляді рівнянь або нерівностей називаються системою обмежень.
Математичне вираження цільової функції та її обмежень називається математичною моделлю економічної задачі або економіко-математичною моделлю.
У загальному вигляді математична модель задачі лінійного програмування можна записати
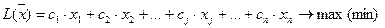
при обмеженнях

де 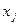 - невідомі,
- невідомі,  - задані сталі величини.
- задані сталі величини.
Всі або декілька рівнянь системи обмежень можуть бути записані у вигляді нерівностей.
Математична модель у більш скороченому вигляді може бути записана

з обмеженнями

Припустимим розв’язком (планом) задачі лінійного програмування називається вектор  , який задовольняє системі обмежень.
, який задовольняє системі обмежень.
Множина припустимих розв’язків утворює область припустимих розв’язків (ОПР).
Припустиме значення, при якому цільова функція досягає свого екстремального значення, називається оптимальним розв’язком задачі лінійного програмування і позначається  .
.
Базисний припустимий розв’язок  є опорним розв’язком, де
є опорним розв’язком, де  - ранг системи обмежень.
- ранг системи обмежень.
Види математичних моделей
Математична модель задачі лінійного програмування може бути представлена у канонічній і неканонічній формі.
Якщо всі обмеження системи задано рівняннями і змінні 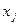 є невід’ємними, тоді таку модель називають канонічною. Якщо хоча б одне обмеження є нерівністю, тоді модель задачі лінійного програмування називають неканонічною.
є невід’ємними, тоді таку модель називають канонічною. Якщо хоча б одне обмеження є нерівністю, тоді модель задачі лінійного програмування називають неканонічною.
Для переходу від неканонічної до канонічної моделі необхідно у кожну нерівність ввести балансову змінну  . Якщо знак нерівності „
. Якщо знак нерівності „  ”, тоді балансова змінна вводиться із знаком „+”, якщо знак нерівності „
”, тоді балансова змінна вводиться із знаком „+”, якщо знак нерівності „  ” - із знаком „-”. У цільову функцію цільові змінні не вводяться.
” - із знаком „-”. У цільову функцію цільові змінні не вводяться.
Таким чином, щоб скласти математичну модель задачі лінійного програмування необхідно:
- ввести позначення змінних;
- виходячи з мети економічних досліджень, скласти цільову функцію;
- враховуючи обмеження у використанні економічних показників задачі та їх кількісні закономірності, записати систему обмежень.
Приклад. Скласти задачу про використання ресурсів.
Нехай на випуск п видів продукції  витрачається т видів ресурсів (сировина, матеріали, праця, тощо)
витрачається т видів ресурсів (сировина, матеріали, праця, тощо) 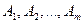 . Відомі витрати
. Відомі витрати  ресурсів і -го виду на одиницю продукції
ресурсів і -го виду на одиницю продукції 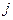 -го виду, обсяг
-го виду, обсяг  ресурсів і -го виду і прибуток
ресурсів і -го виду і прибуток  від реалізації одиниці продукції
від реалізації одиниці продукції 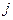 -го виду. Необхідно так організувати випуск продукції, виходячи із наявних ресурсів, щоб одержати найбільший прибуток.
-го виду. Необхідно так організувати випуск продукції, виходячи із наявних ресурсів, щоб одержати найбільший прибуток.
Представимо вихідні дані задачі у вигляді таблиці
Таблиця
| Вид ресурсу | Вид продукції | Запаси ресурсів, грн. | |||||

| 
| ... | 
| ... | 
| ||

| 
| 
| ... | 
| ... | 
| 
|

| 
| 
| ... | 
| ... | 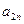
| 
|
| ... | ... | ... | ... | ... | ... | ... | ... |

| 
| 
| ... | 
| ... | 
| 
|
| ... | ... | ... | ... | ... | ... | ... | ... |

| 
| 
| ... | 
| ... | 
| 
|
| Прибуток від реалізації одиниці продукції |

|

| ... |

| ... |

| |
| Випуск продукції | 
| 
| ... | 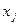
| ... | 
|
За шукані невідомі візьмемо  - кількість одиниць випущеної продукції видів
- кількість одиниць випущеної продукції видів  .
.
Складемо цільову функцію економіко-математичної моделі. Прибуток від випуску всієї продукції становить

Невідомі  повинні задовольняти нерівностям, які показують, що фактичні витрати відповідного виду ресурсів не повинні перевищувати його наявний обсяг
повинні задовольняти нерівностям, які показують, що фактичні витрати відповідного виду ресурсів не повинні перевищувати його наявний обсяг

Виходячи з економічного змісту задачі, невідомі  можуть набувати тільки невід’ємних значень, тобто
можуть набувати тільки невід’ємних значень, тобто 






