Поголовье коров и число ферм на сельскохозяйственных предприятиях

№ сельскохозяйственного предприятия	Число ферм	Поголовье коров, гол.	Среднее поголовье коров на ферме, гол.	Квадрат среднего поголовья коров на ферме
всего	в т. ч. с беспривязным содержанием	хс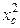
Итого

 

Требуется определить доверительные пределы случайных колебаний поголовья коров на ферме и доли ферм с беспривязным содержанием.

В данном случае произведена серийная выборка. Серия­ми являются сельскохозяйственные предприятия, в которых имеется по нескольку ферм с беспривязным содержанием коров. Поэтому расчеты ведутся по формулам для серийной выборки.

Средние величины для серийной выборки определяют как среднюю арифметическую простую средних величин по каждой серии. Среднее поголовье коров на ферме и доля ферм с беспривязным содержанием:

гол.;

.

Средние квадратические отклонения в выборке:

среднего поголовья коров на ферме:

гол.;

доли ферм с беспривязным содержанием коров:

.

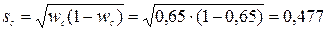Средние ошибки выборки:

среднего поголовья коров на ферме:

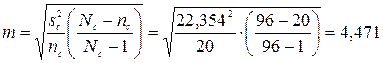гол.;

доли ферм с беспривязным содержанием коров:

.

Нормированное отклонение при доверительном уровне ве­роятности суждения 0,9 равно 1,6449 (табли­ца «Значения интеграла вероятностей при разных значениях t»).

Предельные ошибки выборки:

среднего поголовья коров на ферме:

гол.;

доли ферм с беспривязным содержанием коров:

.

Доверительные пределы:

генерального среднего поголовья коров на ферме:

гол.;

генеральной доли ферм с беспривязным содержанием коров:

.

Полученные данные выборочного наблюдения показыва­ют, что среднее поголовье коров на ферме, по всей совокупности хозяйств находится в пределах 116 ¸ 130,7 гол., а доля ферм с беспривязным содержанием коров - 0,493 ¸ 0,807 при уровне вероятности суждения 0,9.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.27.

 

Р и с. 4.27

2. Рассчитайте общее число ферм в выборке.

2.1. Выделите ячейку D28.

2.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > .

2.3. Выделите ячейки А3:А22.

2.4. Нажмите клавишу <Enter>.

2.5. Аналогично рассчитайте число ферм с беспривязным содержанием коров. Результаты занесите в ячейку D29=СУММ(B3:B22).

3. Рассчитайте среднее поголовье коров на ферме по каждому хозяйству.

3.1. Введите в ячейку D3 формулу =C3/A3.

3.2. Скопируйте ячейку D3 в ячейки D4:D22.

4. Рассчитайте среднее поголовье коров на ферме в целом по выборке.

4.1. Выделите ячейку D30.

4.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

4.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СРЗНАЧ> (рис. 4.28).

 

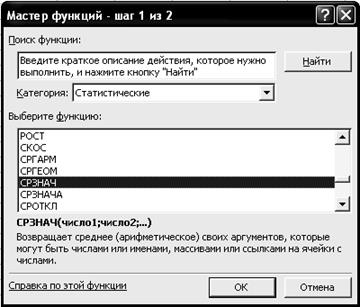
Р и с. 4.28

 

4.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

4.5. На вкладке СРЗНАЧ установите параметры в соответствии с рис. 4.29.

 

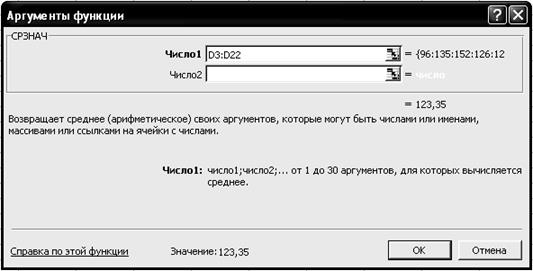
Р и с. 4.29

4.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

5. Рассчитайте среднюю долю ферм с беспривязным содержанием коров. Для этого введите в ячейку D31 формулу =D29/D28.

6. Рассчитайте среднее квадратическое отклонение среднего поголовья коров на ферме, используя статистическую функцию СТАНДОТКЛОН. Для этого вставьте в ячейку D32 функцию =СТАНДОТКЛОН(D3:D22). Порядок вставки изложен в пункте 4.

7. Рассчитайте среднее квадратическое отклонение средней доли ферм с беспривязным содержанием коров. Для этого вставьте в ячейку D33 математическую функцию =КОРЕНЬ(D31*(1-D31)).

8. Рассчитайте средние ошибки выборки среднего поголовья коров на ферме и средней доли ферм с беспривязным содержанием.

8.1. Вставьте в ячейку D34 математическую функцию =КОРЕНЬ(D32^2/$D$27*($D$26-$D$27)/($D$26-1)).

8.2. Скопируйте ячейку D34 в ячейку D35.

9. Рассчитайте предельные ошибки выборки среднего поголовья коров на ферме и средней доли ферм с беспривязным содержанием.

9.1. Введите в ячейку D36 формулу =$D$25*D34.

9.2. Скопируйте ячейку D36 в ячейку D37.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.30).

 

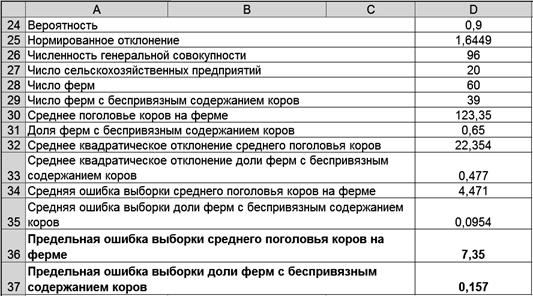
Р и с. 4.30

 

 

3. Определение вероятности осуществления заданной ошибки

Выборочный метод исследования, кроме определения не­обходимой численности выборки и пределов генеральной средней и доли, позволяет определить вероятность осуществ­ления заданной ошибки. Вероятность заданной ошибки опре­деляется с помощью таблицы интеграла вероятностей (при­лож. 1) на основе фактического нормированного откло­нения, которое рассчитывается по формуле:

.

В этом случае надо знать предельную и среднюю ошибки выборки.

Рассмотрим методику расчета вероятности осуществления заданной ошибки при различных способах формирования слу­чайной выборки.

Пример 1. По данным примера 1 в разделе 1 требуется определить, какая будет вероятность осуществления задан­ной ошибки, если численность выборки, характеризующей жи­вую массу цыплят, увеличить вдвое, а численность выборки, характеризующей соотношение петушков и курочек в стаде уменьшить вдвое. В первом случае численность выборки дол­жна быть 50, а во втором - 192.

Расчеты проводят по формулам для случайной повторной выборки.

Средние ошибки выборки:

средней живой массы цыплят:

г;

 

доли петушков или курочек:

.

Отсюда нормированные отклонения:

для средней живой массы цыплят:

;

для доли петушков или курочек:

.

Значению t = 2,75 соответствует вероятность 0,994, а зна­чению t = 1,39 - 0,8355 (табли­ца «Значения интеграла вероятностей при разных значениях t»).

Полученные результаты позволяют сделать вывод, что при увеличении численности выборки вероятность осуществления заданной ошибки повышается, а при уменьшении - понижа­ется. Так, при увеличении численности выборки цыплят при анализе живой массы с 25 до 50 единиц вероятность осуще­ствления заданной ошибки (3,5 г) увеличилась с 0,95 до 0,994. Уменьшение численности цыплят с 384 до 192 голов при оп­ределении доли петушков и курочек при заданной ошибке (0,05) привело к снижению вероятности с 0,95 до 0,8355.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.31.

 

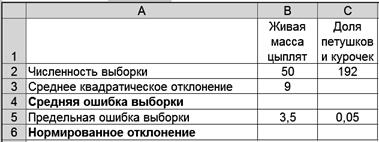
Р и с. 4.31

 

2. Рассчитайте среднее квадратическое отклонение для доли петушков и курочек. Для этого вставьте в ячейку С3 математическую функцию =КОРЕНЬ(0,5*(1-0,5)).

3. Рассчитайте средние ошибки выборки средней живой массы цыплят и доли петушков и курочек.

3.1.Введите в ячейку В4 формулу =B3/КОРЕНЬ(B2).

3.2. Скопируйте ячейку В4 в ячейку С4.

4. Рассчитайте нормированные отклонения для средней живой массы цыплят и доли петушков и курочек.

4.1.Введите в ячейку В6 формулу =B5/B4.

4.2. Скопируйте ячейку В6 в ячейку С6.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.32).

 

Р и с. 4.32

 

Пример 2. По данным примера 2 в разделе 1 требуется определить, какая будет вероятность осуществления заданной ошибки, если ошибку уменьшить вдвое для среднего многоплодия свиноматок и увеличить вдвое для средней доли мертворожденных поросят. В первом случае ошибка вы­борки будет 0,3, а во втором - 0,16, а численность выборки, соответственно, 26 и 32.

Расчеты ведутся по формулам для случайной бесповтор­ной выборки.

Средние ошибки выборки:

среднего многоплодия свиноматок:

гол;

доли мертворожденных поросят:

.

Отсюда нормированное отклонение:

для среднего многоплодия свиноматок:

;

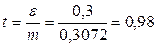для доли мертворожденных поросят:

.

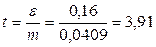Значению t = 0,96 соответствует вероятность 0,6629, а зна­чению t = 3,91 - 0,9996 (табли­ца «Значения интеграла вероятностей при разных значениях t»).

Полученные результаты позволяют сделать вывод, что при неиз­менной численности выборки при уменьшении заданной ошибки вероятность ее осуществ­ления снижается, а при увеличении - повышается. Так, при уменьшении заданной ошибки среднего многоплодия свиней вероятность ее осуществлении снизилась с 0,95 до 0,6629. Увели­чение же ошибки доли мертворожденных поросят вдвое позволило повысить вероятность ее осуществления с 0,95 до 0,9996.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.33.

 

Р и с. 4.33

 

2. Рассчитайте среднее квадратическое отклонение для доли мертворожденных поросят. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,06*(1-0,06)).

3. Рассчитайте средние ошибки выборки среднего многоплодия свиноматок и доли мертворожденных поросят.

3.1.Вставьте в ячейку В5 математическую функцию =КОРЕНЬ(B4^2/B3*(B2-B3)/(B2-1)).

3.2. Скопируйте ячейку В5 в ячейку С5.

4. Рассчитайте нормированные отклонения для среднего многоплодия свиноматок и доли мертворожденных поросят.

4.1.Введите в ячейку В7 формулу =B6/B5.

4.2. Скопируйте ячейку В7 в ячейку С7.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.34).

 

Р и с. 4.34

Пример 3. По данным примера 3 в разделе 1 необходи­мо определить, какая будет вероятность осуществления задан­ной ошибки, если принять ее для средней продуктивности 0,7 кг, а для доли коров с удоем выше среднего - 0,14. При этом для повышения достоверности данных численность вы­борки довести до 50 голов. Среднюю колеблемость суточных удоев коров по группам принять равную 2,28 кг.

Расчеты ведутся по формулам для типической выборки.

Средние ошибки выборки:

среднего суточного удоя коровы:

кг;

доли коров с удоем молока выше среднего:

.

Отсюда нормированное отклонение:

для среднего суточного удоя коровы:

;

для доли коров с удоем молока выше среднего:

.

Значению t = 2,26 соответствует вероятность 0,9762, а значению t = 2,06 - 0,9608 (табли­ца «Значения интеграла вероятностей при разных значениях t»).

Полученные результаты показывают, что, несмотря на уменьшение предельных ошибок выборки, в результате уве­личения численности выборки вероятность осуществления за­данных ошибок повысится. Для среднего суточного удоя коровы вероятность ошибки будет 0,9762, а для до­ли коров с удоем молока выше среднего - 0,9608.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.35.

 

Р и с. 4.35

 

2. Рассчитайте среднее квадратическое отклонение для доли коров с удоем выше и ниже среднего. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,5*(1-0,5)).

3. Рассчитайте средние ошибки выборки среднего суточного удоя молока и доли коров с удоем выше среднего.

3.1.Вставьте в ячейку В5 математическую функцию =КОРЕНЬ(B4^2/B3*(B2-B3)/(B2-1)).

3.2. Скопируйте ячейку В5 в ячейку С5.

4. Рассчитайте нормированные отклонения для среднего суточного удоя молока и доли коров с удоем выше среднего.

4.1.Введите в ячейку В7 формулу =B6/B5.

4.2. Скопируйте ячейку В7 в ячейку С7.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.36).

 

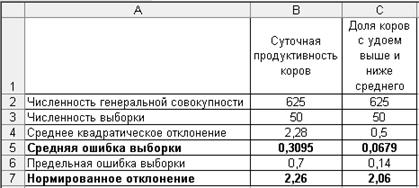
Р и с. 4.36

 

Пример 4. По данным примера 4 в разделе 1 необходи­мо определить, какая будет вероятность осуществления за­данных ошибок, если число серий в выборке довести до 25, то есть увеличить на 25 %.

Расчеты ведутся по формулам для серийной выборки.

Средние ошибки выборки:

среднего поголовья коров на ферме:

гол.;

доли ферм с беспривязным содержанием коров:

.

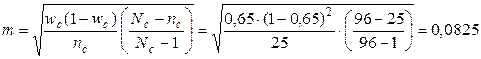Отсюда нормированное отклонение:

для среднего поголовья коров на ферме:

;

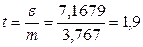для доли ферм с беспривязным содержанием коров:

.

Значение t = 1,9 соответствует вероятности 0,9425 (табли­ца «Значения интеграла вероятностей при разных значениях t»).

При увеличении численности выборки вероятность осуще­ствления заданных ошибок повысилась с 0,9 до 0,9425. Чем больше выборка, тем достовернее ее результаты.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.37.

 

Р и с. 4.37

 

2. Рассчитайте среднее квадратическое отклонение доли звеньев на арендном подряде. Для этого вставьте в ячейку С4 математическую функцию =КОРЕНЬ(0,65*(1-0,65)).

3. Рассчитайте средние ошибки выборки средней площади, обрабатываемой звеном и доли звеньев на арендном подряде.

3.1.Вставьте в ячейку В5 математическую функцию =КОРЕНЬ(B4^2/B3*(B2-B3)/(B2-1)).

3.2. Скопируйте ячейку В5 в ячейку С5.

4. Рассчитайте нормированные отклонения для средней площади, обрабатываемой звеном и доли звеньев на арендном подряде.

4.1.Введите в ячейку В7 формулу =B6/B5.

4.2. Скопируйте ячейку В7 в ячейку С7.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.38).

 

Р и с. 4.38