Многоплодие свиноматок и доля мертворожденных поросят

Живая масса и пол цыплят

Живая масса цыплят, г х	Пол цыплят (петушки - 1, курочки - 0)		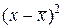	Живая масса цыплят, г х	Пол цыплят (петушки - 1, курочки - 0)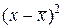
		28,3024 205,062 1,7424 205,062 0,4624 69,2224 2,8224 39,9424 21,9024 11,0224 32,2624 5,3824 0,1024			75,3424 39,9424 114,062 266,342 136,422 160,782 21,9024 245,862 136,422 86,8624 21,9024 28,3024
Итого			1957,44

Требуется определить доверительные пределы случайных колебаний средней живой массы цыплят и доли петушков в стаде при уровне вероятности суждения 0,95.

Определение доверительных пределов состоит в нахождении предельной ошибки, для расчета которой необходимо знать нормированное отклонение, вариацию признака и численность выборки.

Средняя живая масса цыплят и доля петушков в стаде составят соответственно:

г;

Средние квадратические отклонения в выборке:

живой массы цыплят:

г;

доли петушков:

Средние ошибки выборки:

средней живой массы цыплят:

г;

доли петушков:

Нормированное отклонение при доверительном уровне вероятности суждения 0,95 равно 1,96 (таблица «Значения интеграла вероятностей при разных значениях t»).

Отсюда предельные ошибки выборки:

средней живой массы цыплят:

г;

доли петушков в стаде:

Доверительные пределы генеральной средней и генеральной доли будут:

для средней живой массы цыплят:

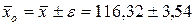г;

для доли петушков в стаде:

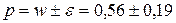Полученные данные позволяют сделать вывод, что средняя живая масса цыплят по всей совокупности находится в пределах от 112,78 г (116,32 - 3,54) до 119,86 г (116,32 + 3,54), а доля петушков от 0,37 (0,56 - 0,19) до 0,75 (0,56 + 0,19). Средняя генеральная доля петушков колеблется в очень больших пределах, что не отражает фактический состав стада, так как доля петушков и курочек в стаде должна быть примерно равна, то есть приближаться к 0,5. Для повышения достоверности расчетных данных необходимо увеличить численность выборки. Это и следует из результатов решения примера 1 в разделе 1.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.9.

Р и с. 4.9

2. Рассчитайте поголовье цыплят.

2.1. Выделите ячейку D30.

2.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СЧЁТ> (рис. 4.10).

Р и с. 4.10

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СЧЁТ установите параметры в соответствии с рис. 4.11.

Р и с. 4.11

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

3. Рассчитайте поголовье петушков.

3.1. Выделите ячейку D31.

3.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

3.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СЧЁТЕСЛИ> (рис. 4.12).

Р и с. 4.12

3.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

3.5. На вкладке СЧЁТЕСЛИ установите параметры в соответствии с рис. 4.13.

Р и с. 4.13

3.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

4. Рассчитайте среднюю живую массу цыплят и долю петушков, используя статистическую функцию СРЗНАЧ. Для этого вставьте в ячейки D32 и D33 функции =СРЗНАЧ(A2:A26) и =СРЗНАЧ(B2:B26). Порядок вставки изложен в пункте 2.

5. Рассчитайте среднее квадратическое отклонение живой массы цыплят, используя статистическую функцию СТАНДОТКЛОН. Для этого вставьте в ячейку D34 функцию =СТАНДОТКЛОН(A2:A26). Порядок вставки изложен в пункте 2.

6. Рассчитайте среднее квадратическое отклонение доли петушков. Для этого вставьте в ячейку D35 формулу =КОРЕНЬ(D33*(1-D33)).

7. Рассчитайте средние ошибки выборки средней живой массы цыплят и доли петушков.

7.1. Введите в ячейку D36 формулу =D34/КОРЕНЬ($D$30).

7.2. Скопируйте ячейку D36 в ячейку D37.

8. Рассчитайте предельные ошибки выборки средней живой массы цыплят и доли петушков.

8.1. Для расчета предельной ошибки выборки средней живой массы цыплят выделите ячейку D38.

8.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

8.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <ДОВЕРИТ> (рис. 4.14).

Р и с. 4.14

8.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

8.5. На вкладке ДОВЕРИТ установите параметры в соответствии с рис. 4.15.

Р и с. 4.15

8.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

8.7. Аналогично рассчитайте предельную ошибку выборки доли петушков (n =25). Результат занесите в ячейку D39.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.16).

Р и с. 4.16

Пример 2. Для анализа многоплодия 600 свиноматок методом случайного бесповторного отбора было отобрано 26 голов. В результате было определено многоплодие каждой свиноматки, а также число мертворожденных поросят (табл. 4.2).

Т а б л и ц а 4.2

Многоплодие свиноматок и доля мертворожденных поросят

Многоплодие свиноматок, гол. х	Число мертворожденных поросят, гол.			Многоплодие свиноматок, гол. х	Число мертворожденных поросят, гол.
		1,8225 0,1225 0,1225 2,7225 2,7225 2,7225 5,5225 1,8225 0,1225 2,7225 2,7225 1,8225 2,7225			2,7225 0,4225 1,8225 1,8225 0,4225 0,1225 7,0225 0,4225 1,8225 5,5225 0,1225 0,1225 1,8225
Итого			51,8850

Необходимо определить пределы случайных колебаний среднего многоплодия свиноматок и доли мертворожденных поросят при уровне вероятности суждения 0,95.

Среднее многоплодие свиноматок в выборке:

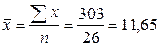гол.

Доля мертворожденных поросят в выборке:

Средние квадратические отклонения в выборке:

среднего многоплодия свиноматок:

гол.;

доли мертворожденных поросят:

Средние ошибки выборки:

среднего многоплодия свиноматок:

гол.;

доли мертворожденных поросят:

Предельные ошибки выборки:

среднего многоплодия свиноматок:

гол.;

доли мертворожденных поросят:

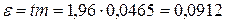Доверительные пределы:

генерального среднего многоплодия свиноматок:

гол.;

генеральной доли мертворожденных поросят:

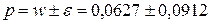Полученные данные выборочного наблюдения показывают, что среднее многоплодие свиноматок по всей совокупности находится в пределах 11,11 ¸ 12,19 гол., а доля мертворожденных поросят, - в пределах −0,0285 ¸ 0,1539. В данном случае велик размах средней доли. К тому же нижняя граница получилось отрицательной. Для получения более достоверных результатов необходимо увеличить объем выборки.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.17.

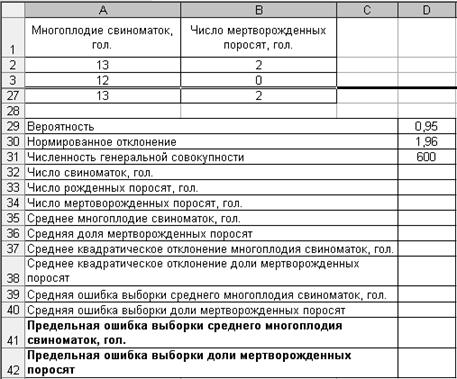
Р и с. 4.17

2. Рассчитайте число свиноматок.

2.1. Выделите ячейку D32.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СЧЁТ> (рис. 4.18).

Р и с. 4.18

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СЧЁТ установите параметры в соответствии с рис. 4.19.

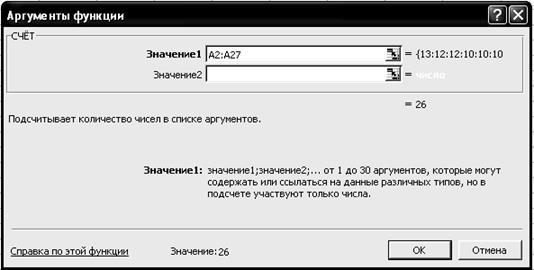
Р и с. 4.19

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

3. Рассчитайте число рожденных поросят.

3.1. Выделите ячейку D33.

3.2. Щелкните левой кнопкой мыши на панели инструментов на букве S кнопки <Автосумма > .

3.3. Выделите ячейки А2:А27.

3.4. Нажмите клавишу <Enter>.

3.5. Аналогично рассчитайте число мертворожденных поросят. Результат занесите в ячейку D34=СУММ(B2:B27).

4. Рассчитайте среднее многоплодие свиноматок, используя статистическую функцию СРЗНАЧ. Для этого вставьте в ячейки D35 функцию =СРЗНАЧ(A2:A27). Порядок вставки изложен в пункте 2.

5. Рассчитайте среднюю долю мертворожденных поросят. Для этого введите в ячейку D36 формулу =D34/D33.

6. Рассчитайте средние квадратическое отклонение среднего многоплодия свиноматок, используя статистическую функцию СТАНДОТКЛОН. Для этого вставьте в ячейку D37 функцию =СТАНДОТКЛОН(A2:A27). Порядок вставки изложен в пункте 2.

7. Рассчитайте среднее квадратическое отклонение средней доли мертворожденных поросят. Для этого вставьте в ячейку D38 математическую функцию =КОРЕНЬ((1-D36)*D36).

8. Рассчитайте средние ошибки выборки среднего многоплодия свиноматок и доли мертворожденных поросят.

8.1. Вставьте в ячейку D39 математическую функцию =КОРЕНЬ(D37^2/$D$32*($D$31-$D$32)/($D$31-1)).

8.2. Скопируйте ячейку D39 в ячейку D40.

9. Рассчитайте предельные ошибки выборки многоплодия свиноматок и доли мертворожденных поросят.

9.1. Введите в ячейку D41 формулу =$D$30*D39.

9.2. Скопируйте ячейку D41 в ячейку D42.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.20).

Р и с. 4.20

Пример 3. Для обследования продуктивности стада коров (625 голов) было проведено типическое выборочное наблюдение. Объем выборки составил 28 голов. Стадо подразделено на три группы по породности и внутри групп пропорционально численности в общей совокупности произведен механический отбор. В первую группу (чистопородные) вошло 14, во вторую (высококровные) - 8 и в третью (помеси низкокровные) - 6 коров (табл. 4.3).

Требуется определить доверительные пределы случайных колебаний среднего суточного удоя молока и доли коров с удоем выше среднего при уровне вероятности суждения 0,95.

Т а б л и ц а 4.3

Суточный удой коровы

Породность	Суточный удой, кг х			Породность	Суточный удой, кг х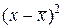
Чистопородные (группа 1)	20,2	2,629	Высококровные (группа 2)	19,3	0,170
	3,318	21,1	1,925
25,8	15,829	17,2	6,313
22,6	0,606	17,0	7,358
23,8	3,915	18,8	0,833
18,5	11,032	23,6	15,113
25,1	10,749	20,4	0,473
23,7	3,529	20,3	0,345
20,4	2,020	Итого	157,7	32,529
20,6	1,492	Помеси низкокровные (группа 3)	15,2	4,203
19,7	4,500	20,9	13,323
20,4	2,020	20,4	9,922
24,9	9,478	14,6	7,023
19,8	4,086	15,6	2,723
Итого	305,5	75,204	16,8	0,202
			Итого	103,5	37,395

Расчеты ведутся по формулам для типической выборки.

Средний суточный удой коровы и доля коров с удоем выше среднего по выборочным группам составят:

группа 1:

кг;

;

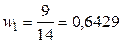группа 2:

кг;

;

группа 3:

кг;

В целом по совокупности:

кг;

Дисперсия по группам:

группа 1:

для среднего суточного удоя коровы:

;

для доли коров с удоем выше среднего:

;

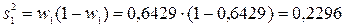группа 2:

для среднего суточного удоя коровы:

;

для доли коров с удоем выше среднего:

;

группа 3:

для среднего суточного удоя коровы:

;

для доли коров с удоем выше среднего:

Средняя выборочная дисперсия и среднее выборочное квадратическое отклонение по выборочной совокупности равны:

для среднего суточного удоя коровы:

;

кг;

для доли коров с удоем выше среднего:

;

Средние ошибки выборки:

среднего суточного удоя коровы:

кг;

доли коров с удоем выше среднего:

Предельные ошибки выборки:

среднего суточного удоя коровы:

кг;

доли коров с удоем выше среднего:

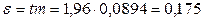Доверительные пределы:

генерального среднего суточного удоя коровы:

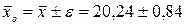кг;

генеральной доли коров с удоем выше среднего:

Полученные данные выборочного наблюдения показывают, что средний суточный удой коровы по всей совокупности находится в пределах 19,40 ¸ 21,08 кг, а доля коров с суточным удоем молока выше среднего - в пределах 0,361 ¸ 0,711 при уровне вероятности суждения 0,95. Пределы колебаний доли коров показывают, что в стаде может быть от 36,1 до 71,1 % коров с удоем молока выше среднего. Фактически же доля коров с удоем молока выше среднего составляет около 50 %. Для уменьшения пределов генеральной средней и доли необходимо увеличить численность выборки.

Технология решения задачи втабличном процессоре Microsoft Excel следующая.

1. Введите исходные данные в соответствии с рис. 4.21.

Р и с. 4.21

2. Рассчитайте поголовье коров в группах и в целом по выборке.

2.1. Выделите ячейку С35.

2.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СЧЁТ> (рис. 4.22).

Р и с. 4.22

2.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.5. На вкладке СЧЁТ установите параметры в соответствии с рис. 4.23.

Р и с. 4.23

2.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

2.7. Аналогично рассчитайте поголовье коров в остальных группах и в целом по выборке. Для этого вставьте в ячейки D35, E35 и F35 статистические функции =СЧЁТ(B16:B23), =СЧЁТ(B24:B29) и =СЧЁТ(B2:B29).

3. Рассчитайте средний суточный удой молока по группам и в целом по выборке, используя статистическую функцию СРЗНАЧ. Для этого вставьте в ячейки С37, D37, E37 и F38 функции =СРЗНАЧ(B2:B15), =СРЗНАЧ(B16:B23), =СРЗНАЧ(B24:B29) и =СРЗНАЧ(B2:B29). Порядок вставки изложен в пункте 2.

4. Рассчитайте поголовье коров с удоем выше среднего в группах и в целом по выборке.

4.1. Выделите ячейку С36.

4.2. Щелкните левой кнопкой мыши на панели инструментов на кнопке <Вставка функции> или выполните команду Вставка, f_x Функция, щелкнув поочередно левой кнопкой мыши.

4.3. В диалоговом окне Мастер функций - шаг 1 из 2 с помощью левой кнопки мыши установите: Категория ® <Статистические>, Выберете функцию ® <СЧЁТЕСЛИ> (рис. 4.24).

Р и с. 4.24

4.4. Щелкните левой кнопкой мыши на кнопке <ОК>.

4.5. На вкладке СЧЁТЕСЛИ установите параметры в соответствии с рис. 4.25.

Р и с. 4.25

4.6. Щелкните левой кнопкой мыши на кнопке <ОК>.

4.7. Аналогично рассчитайте поголовье коров выше среднего в остальных группах и в целом по выборке. Для этого вставьте в ячейки D36, E36 и F36 статистические функции =СЧЁТЕСЛИ(B16:B23;">20,24"), =СЧЁТЕСЛИ(B24:B29;">20,24") и =СЧЁТЕСЛИ(B2:B29;">20,24").

5. Рассчитайте среднюю долю коров с удоем выше среднего по группам и в целом по выборке.

5.1. Введите в ячейку С38 формулу =C36/C35.

5.2. Скопируйте ячейку С38 в ячейки D38:F38.

6. Рассчитайте дисперсии среднего суточного удоя молока по группам, используя статистическую функцию ДИСП. Для этого вставьте в ячейки С39 D39 и E39 функции =ДИСП(B2:B15), =ДИСП(B16:B23) и =ДИСП(B24:B29). Порядок вставки изложен в пункте 2.

7. Рассчитайте дисперсии доли коров с удоем выше среднего по группам.

7.1. Введите в ячейку С40 формулу =C38*(1-C38).

7.2. Скопируйте ячейку С40 в ячейки D40:F40.

8. Рассчитайте средние выборочные дисперсии среднего суточного удоя молока и доли коров с удоем выше среднего в целом по выборке.

8.1. Вставьте в ячейку F39 математическую функцию =СУММПРОИЗВ($C$35:$E$35;C39:E39)/$F$35.

8.2. Скопируйте ячейку F39 в ячейку F40.

9. Рассчитайте средние выборочные отклонения среднего суточного удоя молока и доли коров с удоем выше среднего в целом по выборке.

9.1. Вставьте в ячейку F41 математическую функцию =КОРЕНЬ(F39).

9.2. Скопируйте ячейку F41 в ячейку F42.

10. Рассчитайте средние ошибки выборки среднего суточного удоя молока и доли коров с удоем выше среднего в целом по выборке.

10.1. Вставьте в ячейку F43 математическую функцию =КОРЕНЬ(F39/$F$35*($F$34-$F$35)/($F$34-1)).

10.2. Скопируйте ячейку F43 в ячейку F44.

11. Рассчитайте предельные ошибки выборки среднего суточного удоя молока и доли коров с удоем выше среднего в целом по выборке.

11.1. Введите в ячейку F45 формулу =$F$33*F43.

11.2. Скопируйте ячейку F45 в ячейку F46.

Результаты решения выводятся на экран дисплея в следующем виде (рис. 4.26).

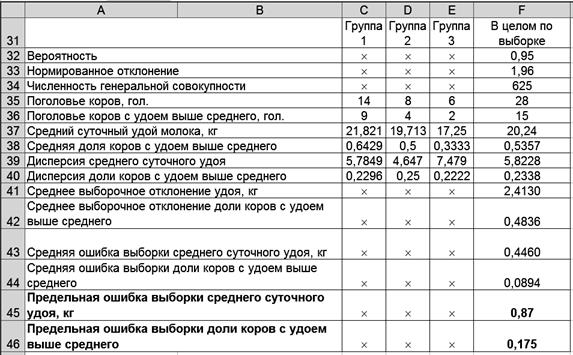
Р и с. 4.26

Пример 4. Для характеристики ферм с беспривязным содержанием коров, было проведено выборочное обследование. Из 96 сельскохозяйственных предприятий способом механического отбора сделана выборка в 20 хозяйствах. Поголовье коров и число ферм представлены в табл. 4.4.

Т а б л и ц а 4.4