4.1. Бинарная операция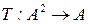 
заданана множестве 
. Определить ее свойства, если 
.
Решение.
Проверим коммутативность. Для этого следует убедиться, что для всех 
, 
R выполняется равенство 
.
Поскольку 
, а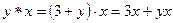 
, то условие коммутативности примет вид: 
, что равносильно тому, что 
.
Ясно, что это равенство выполняется не всегда. Следовательно, заданная операция некоммутативна.
Проверим теперь ассоциативность операции, то есть выясним, при каких x, y, z имеет место равенство 
.
Точнее, нас интересует только один факт: при всех ли значениях переменных это равенство справедливо. Преобразуем выражения:
;
.
Очевидно, что полученные выражения не всегда дают равные значения. Приведем контрпример.
Пусть 
, 
, 
. Тогда:
;
.
Следовательно, ассоциативность не выполняется.
4.2 Задано отображение 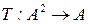на множестве 
. Является ли оно бинарной операцией, если 
?
Решение.
Пусть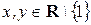 
. Поскольку арифметические действия умножения, сложения и вычитания однозначно определены для любых действительных чисел, то ясно, что 
определено однозначно и 
. Покажем, что 
. Предположим, что 
, т.е. 
. Тогда, упростив, получаем 
. Получаем противоречие, так как 
. Полученное противоречие показывает, что . Следовательно, 
, и правило * есть бинарная операция.
4.3. На множестве действительных чисел определена бинарная операция (*) следующим образом: 
. Найти корень уравнения 
.
Решение.
Имеем:
,
,
.
4.4. Примеры операций над множествами.
Решение.
1) Пусть 
Тогда 
2) Пусть 
Тогда 
3) Пусть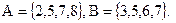 
Тогда 
4) Пусть 
Тогда 
4.5 Найти образ и ядро оператора, заданного матрицей A = 
.
Решение.
Область значений оператора - образ-– это множество всех векторов
.
Ядро линейного оператора – это множество всех векторов, которые А отображает в нуль-вектор, т.е. решение 
:
.
4.6. Найти матрицу и образ оператора А, действующего в R3 следующим образом:
.
Решение:
Матрица оператора имеет вид:
.
Образ оператора
