Тренировочные задачи и упражнения
Специальность ИВТ
Дисциплина алгебра и геометрия
Семестр
2012-2013
Модуль 1
Линейная алгебра.
1.1. Даны матрицы А =  ; B =
; B =  , найти 2А + В.
, найти 2А + В.
Решение. 2А =  , 2А + В =
, 2А + В =  .
.
1.2. Даны матрицы А =  , В =
, В =  , С =
, С =  и число a = 2. Найти АТВ+aС.
и число a = 2. Найти АТВ+aС.
Решение. AT =  ;
;
ATB =  ×
×  =
=  =
=  ; aC =
; aC =  ;
;
АТВ+aС =  +
+  =
=  .
.
1.3 Вычислить определитель матрицы А = 
Решение: 
= -5 + 18 + 6 = 19.(раскладывали по 1 строке.)
1.4. Найти значение матричного многочлена  если
если  .
.
Решение.
 .
.
1.5. Определить ранг матрицы  .
.
Решение:
 ~1 стр.+3 стр ~
~1 стр.+3 стр ~  ~ 1стр.-2стр*4~
~ 1стр.-2стр*4~  ~1стр-2стр, нулевую отбрасываем~
~1стр-2стр, нулевую отбрасываем~  ,
,  rang (А) = 2.
rang (А) = 2.
1.6 Определить след, норму матрицы  .
.
Решение:
 (сумма диагональных элементов)
(сумма диагональных элементов)

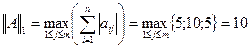


1.7 Решить систему уравнений матричным методом:

Решение:
Х =  , B =
, B =  , A =
, A = 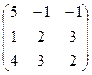
Найдем обратную матрицу А-1.
D = det A =  5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9) + 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
А11 =  = -5; А21 = -
= -5; А21 = -  = -1; А31 =
= -1; А31 =  = -1;
= -1;
А12 = -  А22 =
А22 =  А32 = -
А32 = - 
А13 =  А23 = -
А23 = -  А33 =
А33 = 
 A-1 =
A-1 =  ;
;
Сделаем проверку:
A×A-1 = 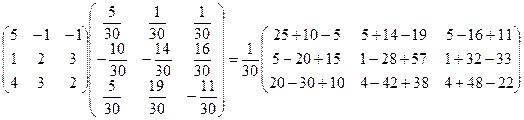 =E.
=E.
Находим матрицу Х.
Х =  = А-1В =
= А-1В =  ×
×  =
=  .
.
Итого решения системы: x =1; y = 2; z = 3.
1.8. Найти число обусловленности матрицы A = 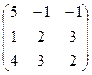
Решение.
Ранее нашли. A-1 =  ;
;
 ;
;
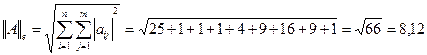


1.9 Найти решение системы уравнений Методом Крамера:

Решение:
D =  = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
Dx =  = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x = Dx/D = 1;
Dy =  = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
y = Dy/D = 2;
Dz =  = 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.
z = Dz/D = 3.
1.10 Решить систему линейных уравнений методом Гаусса.

Решение:
Составим расширенную матрицу системы и преобразуем при помощи элементарных преобразований.
А* = 
Таким образом, исходная система может быть представлена в виде:
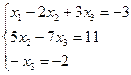 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
1.11. Найти собственные числа и собственные векторы оператора, заданного матрицей  .
.
Решение.
Составим характеристическое уравнение  имеет вид
имеет вид  , получаем
, получаем  - собственные числа.
- собственные числа.
Решая для каждого собственного числа систему  находим соответствующие им собственные векторы
находим соответствующие им собственные векторы  ,
,  .
.
1.12.. Найдите собственные числа и собственные векторы оператора, заданного матрицей  .
.
Решение.
Составляем характеристическую матрицу  :
:

Решаем характеристическое уравнение 
 .
.
Подбором находим один из корней -1.
Так как число -1 является корнем многочлена  , то многочлен
, то многочлен  делится на разность
делится на разность  , то есть
, то есть  , где
, где  - многочлен. Выделим в характеристическом многочлене множитель
- многочлен. Выделим в характеристическом многочлене множитель  :
: 
Находим корни трехчлена  . Они равны -1 и 3. Таким образом,
. Они равны -1 и 3. Таким образом,
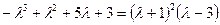
 - корень кратности 2,
- корень кратности 2,  - простой корень. Итак, собственные числа матрицы
- простой корень. Итак, собственные числа матрицы  равны
равны  ,
,  . Найдем соответствующие им собственные векторы.
. Найдем соответствующие им собственные векторы.
Пусть  , тогда для собственного вектора X получаем матричное уравнение
, тогда для собственного вектора X получаем матричное уравнение 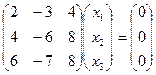 ,
,
что соответствует системе уравнений

Решаем ее методом Гаусса. Выписываем расширенную матрицу системы
 .
.
Первую строку, умноженную на числа -2 и -3 прибавляем соответственно ко второй и третьей строкам
 .
.
Меняем местами вторую и третью строки
 .
.
Возвращаемся к системе уравнений  .
.
Ранг матрицы  равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные
равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные  оставляем в левой части, а переменную
оставляем в левой части, а переменную 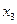 переносим в правую часть
переносим в правую часть
 .
.
Полагаем  , находим
, находим 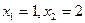 . Итак, собственному числу
. Итак, собственному числу  соответствует собственный вектор
соответствует собственный вектор  .
.
Пусть  , тогда для собственного вектора
, тогда для собственного вектора  получаем матричное уравнение
получаем матричное уравнение
 ,
,
что соответствует системе уравнений
 .
.
Решаем ее методом Гаусса. Выписываем расширенную матрицу

Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам

Вторую строку умножаем на -1 и прибавляем к третьей

Возвращаемся к системе уравнений

Ранг матрицы  равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные
равен 2. Число уравнений равно 2 (число линейно независимых строк), а число неизвестных 3. Поэтому фундаментальная система содержит только одно (3-2=1) решение. Переменные  оставляем в левой части, а переменную
оставляем в левой части, а переменную 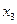 переносим в правую часть
переносим в правую часть
 .
.
Полагаем  , находим
, находим  . Итак, собственному числу
. Итак, собственному числу  соответствует собственный вектор
соответствует собственный вектор  .
.
. Чтобы избавиться от дроби, умножим собственный вектор на 2, получим собственный вектор с тем же самым собственным числом. В итоге собственному числу  соответствует собственный вектор
соответствует собственный вектор  .
.
1.13. Найти фундаментальную систему решений

Решение.
1. В системе выражаем r – базисных переменных (с отличным от нуля базисным минором) через свободные.
 ~
~ 
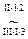

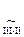

r(A) = r = 2
n = 4 k = n – r = 2
Фундаментальная система решений имеет k = 2
 - базисные
- базисные
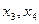 - свободные
- свободные




2. Поочередно заменяем n – r свободных переменных строками единичной матрицы  .
.

1) 


2) 



фундаментальная система решений 

Общее решение
 .
.






