2.1 Даны векторы 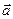 (1; 2; 3),
(1; 2; 3),  (-1; 0; 3),
(-1; 0; 3),  (2; 1; -1) и
(2; 1; -1) и 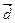 (3; 2; 2) в некотором базисе. Показать, что векторы
(3; 2; 2) в некотором базисе. Показать, что векторы 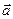 ,
,  и
и  образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 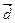 в этом базисе.
в этом базисе.
Решение. Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:
 линейно независимы.
линейно независимы.
Тогда  .
.
Это условие выполняется, если определитель матрицы системы отличен от нуля.
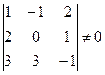
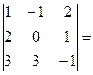

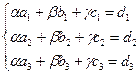
Для решения этой системы воспользуемся методом Крамера.
D1 = 
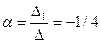 ;
;
D2 = 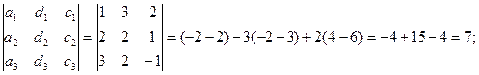
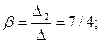
D3 = 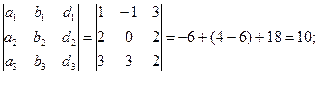
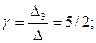
Итого, координаты вектора 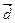 в базисе
в базисе 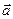 ,
,  ,
,  :
: 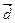 = { -1/4, 7/4, 5/2}.
= { -1/4, 7/4, 5/2}.
2.2 Найти (5 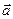 + 3
+ 3  )(2
)(2 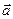 -
-  ), если
), если 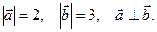
Решение.
10 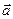 ×
× 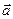 - 5
- 5 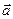 ×
×  + 6
+ 6 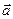 ×
×  - 3
- 3  ×
×  = 10
= 10 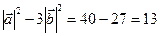 ,
,
т.к. 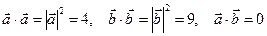 .
.
2.3 Найти угол между векторами 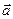 и
и  , если
, если 
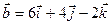 .
.
Решение.
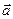 = (1, 2, 3),
= (1, 2, 3),  = (6, 4, -2)
= (6, 4, -2)
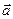 ×
×  = 6 + 8 – 6 = 8:
= 6 + 8 – 6 = 8:
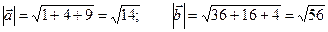 .
.
cosj = 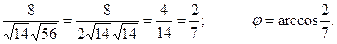
2.4 Найти векторное произведение векторов  и
и
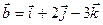 .
.
Решение.
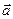 = (2, 5, 1);
= (2, 5, 1);  = (1, 2, -3)
= (1, 2, -3)
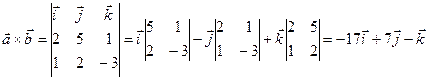 .
.
2.5 Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
Решение.

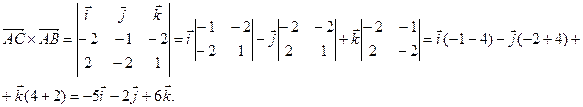
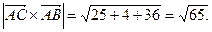

2.6 Найти площадь параллелограмма, построенного на векторах 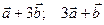 , если
, если 
Решение.

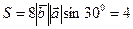 (ед2).
(ед2).
2.7 Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Решение.
Найдем координаты векторов: 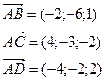
Найдем смешанное произведение полученных векторов:
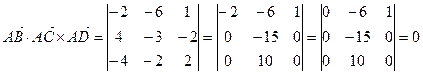 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
2.8 Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0;0;1), B(2;3;5), C(6;2;3), D(3;7;2).
Решение.
Найдем координаты векторов: 
Объем пирамиды 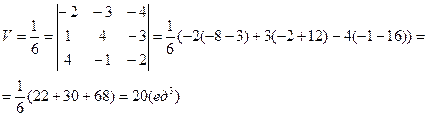
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
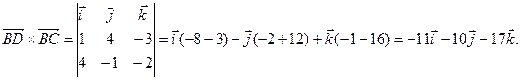

Sосн = 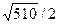 (ед2)
(ед2)
Т.к. V = 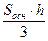 ;
; 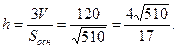 (ед)
(ед)
2.9. Найти координаты вектора 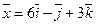 в пространстве R3 -- трехмерном векторном пространстве, в новом базисе
в пространстве R3 -- трехмерном векторном пространстве, в новом базисе 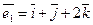 ,
,  ,
, 
Решение.
Выпишем матрицу перехода, ее столбцы -- это координаты новых базисных векторов

Пусть  - координатный столбец вектора
- координатный столбец вектора 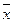 в новом базисе. Тогда
в новом базисе. Тогда  , откуда
, откуда 
Находим определитель 
Находим алгебраические дополнения и обратную матрицу
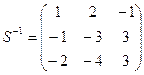 .
.
Находим координаты вектора 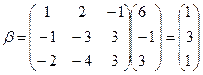 .
.
Таким образом, новые координаты вектора 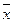 :
: 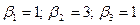 ,
, 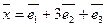
Тот же самый результат можно было получить, записав систему уравнений
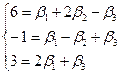
Решив эту систему, например, методом Гаусса, найдем новые координаты 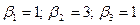 .
.






