3.1 Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору 
(3, -1).
Решение.
Воспользуемся общим уравнением прямой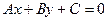 
. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
3.2 Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Решение.
Уравнение прямой имеет вид: 
, a = b = 1; ab/2 = 8; a = 4; -4.
a = -4 не подходит по условию задачи.
Итого: 
или х + у – 4 = 0.
3.3 Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Решение.
Уравнение прямой имеет вид: 
, где х1 = у1 = 0; x2 = -2; y2 = -3.
3.4 Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
Решение. Угол между двумя прямыми, заданными уравнениями с угловыми коэффициентами 
, 
определяется по формуле: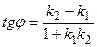 
.
k1 = -3; k2 = 2 tgj = 
; j = p/4.
3.5 Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Решение.
Находим уравнение стороны АВ: 
; 4x = 6y – 6;
2x – 3y + 3 = 0; 
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k = 
. Тогда y =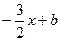 
. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 
откуда b = 17. Итого: 
.
Ответ: 3x + 2y – 34 = 0.
Кривые 2 порядка.
3.6 Найти координаты центра и радиус окружности, если ее уравнение задано в виде 2x2 + 2y2 – 8x + 5y – 4 = 0.
Решение. Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к каноническому виду. Для этого выделим полные квадраты:
x2 + y2 – 4x + 2,5y – 2 = 0
x2 – 4x + 4 –4 + y2 + 2,5y + 25/16 – 25/16 – 2 = 0
(x – 2)2 + (y + 5/4)2 – 25/16 – 6 = 0
(x – 2)2 + (y + 5/4)2 = 121/16
Отсюда находим О(2; -5/4); R = 11/4.
3.7 Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
Решение. Уравнение эллипса имеет вид: 
. Расстояние между фокусами:
2c = 
, таким образом, a2 – b2 = c2 = ½
по условию 2а = 2, следовательно а = 1, b =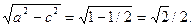 
Итого: 
.
3.8 Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 
Решение. Находим фокусное расстояние c2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c/a = 2; c = 2a; c2 = 4a2; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 
- искомое уравнение гиперболы.
3.9 На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4.
Решение. Из уравнения параболы 
получаем, что р = 4.
r = x + p/2 = 4; следовательно:
x = 2; y2 = 16; y = ±4. Искомые точки: M1(2; 4), M2(2; -4).
3.10. Привести к каноническому виду уравнение второго порядка
.
Решение.
Матрица квадратичной формы 
имеет вид: 
.
Найдем ее собственные числа и собственные векторы. Составим характеристическое уравнение: 
, 
.
Для координат собственного вектора 
, соответствующего λ1, получим с учетом нормировки: 
, откуда = 
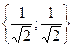. Аналогично найдем 
, = 
.
Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов: 
.
Тогда 
.
Подставив эти выражения в исходное уравнение, получим его вид в новой системе координат: 
. Заметим, что коэффициентами при x² и y² являются λ1 и λ2.
Преобразуем полученное уравнение:
,
.
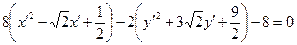Зададим параллельный перенос формулами: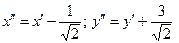 
.
Получим уравнение: 
, а после деления на 8: 
- каноническое уравнение гиперболы.
3.11. Определить тип кривой, заданной уравнением 
, ее параметры и сделать рисунок.
Решение.
Сгруппируем переменные: 
.
Дополним выражения, стоящие в скобках, до полного квадрата: 
,
Получим:
Уравнение определяет гиперболу с центром в точке 
и полуосями 
. Оси данной гиперболы будут лежать на прямых 
.
Определим параметр 
:
.
Тогда эксцентриситет будет равен: 
.
Асимптотами гиперболы будут прямые 
, или, после очевидных преобразований 
.
Директрисами гиперболы будут прямые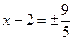 
, или, что то же самое, прямые 
.
3.12. Найти координаты точки М(-4;2) в новой системе координат, полученной поворотом осей на 30° и переносом начала координат в точку А(6;-2).
Решение.
Используем формулы перехода
.
У нас
.
Решаем систему, находим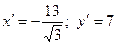 
, т.е. 
.
Прямая и плоскость в пространстве.
3.13 Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость
Решение.
Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:
A(x – x0) + B(y – y0) + C(z – z0) = 0.
3.14 Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2 z – 3 = 0.
Решение. Искомое уравнение плоскости имеет вид: A x + B y + C z + D = 0, вектор нормали к этой плоскости 
(A, B, C). Вектор 
(1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой, имеет вектор нормали 
(1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 - 2×4 + D = 0; D = -21.
Итого, получаем уравнение плоскости: 11 x - 7 y – 2 z – 21 = 0.
3.15 Привести к каноническому виду уравнение прямой, заданное в виде:
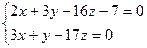
Решение.
Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:
;
2x – 9x – 7 = 0;
x = -1; y = 3;
Получаем: A(-1; 3; 0).
Направляющий вектор прямой: 
.
Итого: 
3.16 Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2; 1; 1), A4(1; 2; 5).
1. Найти длину ребра А1А2.
Решение.
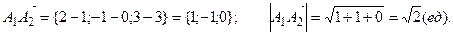
2. Найти угол между ребрами А1А2 и А1А4.
Решение.
3. Найти угол между ребром А1А4 и гранью А1А2А3.
Решение. Сначала найдем вектор нормали 
к грани А1А2А3 как векторное произведение векторов 
и 
.
= (2-1; 1-0; 1-3) = (1; 1; -2);
Найдем угол между вектором нормали и вектором 
.
-4 – 4 = -8.
Искомый угол g между вектором и плоскостью будет равен g = 900 - b.
4. Найти уравнение плоскости А1А2А3.
Решение. Воспользуемся формулой уравнения плоскости, проходящей через три точки.
2x + 2y + 2z – 8 = 0
x + y + z – 4 = 0.
