3.17. Определить вид и параметры поверхности второго порядка, заданной уравнением
Решение. Преобразуем это уравнение, выделив в левой части полные квадраты:
Введем новые координаты по формулам:
(I)
Тогда уравнение примет вид
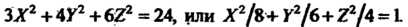
Полученное уравнение определяет эллипсоид, для которого 
Центр эллипсоида находится в точке 
В новой системе
Координат центром является точка с координатами 
Из этих равенств и формул (I) находим 
Т. е. координаты точки 
3.18. Определить вид и параметры поверхности
Решение. Преобразуем это уравнение:
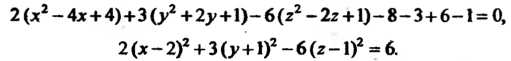
Переходя к новым координатам по формулам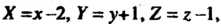 
Получаем
Или 
Это уравнение определяет однополостный гиперболоид, для которого 
С центром в точке 
3.19. Доказать, что уравнение 
Определяет гиперболический параболоид.
Решение. Введем новые координаты по формулам 
Тогда Уравнение примет вид 
Полученное уравнение является уравнением вида x2/a2-y2/b2=2z, для которого 
, 
; оно определяет гиперболический параболоид.
3.20 Приведите уравнение поверхности
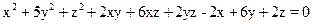
к каноническому виду.
Решение. Квадратичная форма имеет вид
Выписываем ее матрицу
.
Находим ее собственные числа. Для этого запишем характеристическое уравнение
.
После вычисления определителя получим 
.
Подбором находим один корень 
. Преобразуем уравнение, выделяя множитель 
или 
.
Находим два других корня характеристического уравнения 
и 
.
Находим собственные векторы. Для собственного числа для координат собственного вектора 
получим систему уравнений
Решая ее находим, что фундаментальная система решений содержит только одно решение, и в качестве собственного вектора можно взять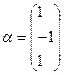 
.
Для собственного числа находим собственный вектор 
.
Для собственного числа находим собственный вектор 
.
Легко проверить, что 
, то есть собственные векторы попарно ортогональны. Их длины равны соответственно 
. Поэтому векторы нового ортонормированного базиса будут иметь координаты
, 
, 
Матрица перехода имеет вид
.
Старые координаты связаны с новыми уравнением 
, то есть
,
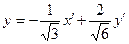
Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа
Приводим подобные члены
Выделим полные квадраты
Выполняем параллельный перенос осей координат
Новое начало системы координат О1 имеет координаты
В исходной системе координат точка О1 (подставляем в формулы замены) имеет координаты
Получили уравнение однополостного гиперболоида.
