Пусть некоторый объект характеризуется двумя признаками. Между признаками Х и Y могут существовать различные виды зависимостей.
Функциональная зависимость, когда каждому значению признака X соответствует единственное значение признака Y. Зависимость задается в виде функции 
.
Статистическая зависимость, когда каждому значению признака X соответствует статистическое распределение признака Y. Зависимость задается в виде корреляционной таблицы.
Корреляционная зависимость - это частный случай статистической зависимости, когда каждому значению признака X соответствует среднее значение признака Y: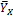 
и связь между ними достаточно хорошо описывается функцией 
, называемой уравнением регрессии Y по X. Аналогично каждому значению Y соответствует среднее значение признака. X: 
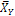и эта зависимость описывается в виде функции 
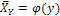, называемой уравнением регрессии X по Y.
Корреляционная зависимость задается уравнением регрессии.
Две основные задачи теории корреляции:
1) Оценить силу (тесноту) связи между признаками Х и Y;
2) Найти вид (форму) этой связи в виде уравнения регрессии.
Наиболее простой и употребляемый вид связи - линейная связь. Она задается уравнением линейной регрессии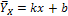 
и изображается на графике в виде прямой регрессии.
Пример
По данным корреляционной таблицы найти условные средние 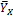и 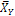. Оценить тесноту линейной связи между признаками 
и 
и составить уравнения линейной регрессии по и по . Оценить силу связи между признаками с помощью корреляционного отношения.
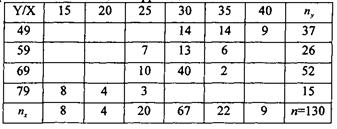
Решение: В таблице, данной по условию задачи, приведены полученные в результате выборочных наблюдений значения признака X (верхняя горизонтальная строка) и признака Y (первый вертикальный столбец). Каждой паре значений (X;Y) соответствует частота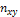 
, стоящая на пересечении соответствующих строки и столбца. Частота 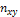показывает, сколько раз наблюдается каждая пара значений.
Например: пара значений 
наблюдалась 8 раз, пара значений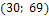 
наблюдалась 40 раз и т.д.
Пустые клетки означают, что соответствующие им пары значений не наблюдались.
В нижней итоговой строке данной таблицы напротив каждого значения признака X проставляется соответствующая ему частота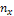 
, равная сумме всех частот столбца и указывающая, сколько раз всего наблюдается данное значение X. Аналогично в последнем итоговом столбце напротив каждого значения Y записывают соответствующую ему частоту 
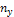, равную сумме частот по строке и указывающую, сколько раз всего наблюдалось данное значение Y. Очевидно, что суммы всех частот 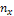для и для 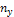должны быть равны между собой и показывать объем выборки (количество наблюдаемых пар):
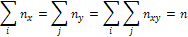
Объем выборки 
представляется в последней клетке таблицы.
В таблице каждому значению X соответствует статистическое распределение признака У.
Например, для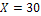 
:
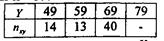
Отсюда находим среднее значение Y при условии, что Х = 30, или условную среднюю:
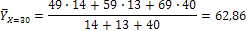
Аналогично каждому значению Y соответствует статистическое распределение по X.
Например, для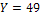 
:
Отсюда находим среднюю условную:
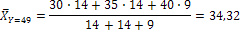
Не выписывая далее статистических распределений, а, беря их непосредственно из данной корреляционной таблицы, найдем все условные средние по формулам: 
, 
,
;
;
;
;
;
;
;
;
;
.
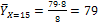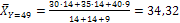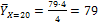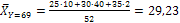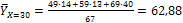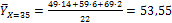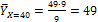Оценка тесноты линейной связи между признаками X и Y производится с помощью коэффициента линейной корреляции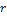 
:
.
Коэффициент 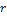может принимать значения от -1 до +1, то есть: 
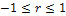или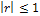 
.
Знак 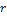указывает на вид связи: прямая или обратная. Абсолютная величина 
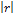указывает на силу (тесноту) связи.
При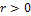 
связь прямая, то есть с ростом X растет Y.
При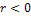 
связь обратная, то есть с ростом X убывает Y.
Для нахождения 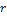вычислим указанные общие средние: 
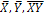а также средние квадратические отклонения 
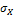и 
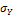. Вычисления удобно поместить в таблицах 2 и 3, куда вписываем также найденные ранее условные средние.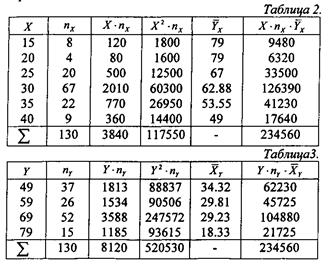 
Контроль: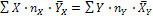 
.
В рассматриваемой задаче эта сумма в обеих таблицах равна 234560. Равенство может оказаться приближенным, что связано с приближенными вычислениями условных средних 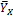и .
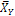С помощью таблиц 2 и 3 находим общие средние, средние квадратов, среднюю произведения и средние квадратические отклонения:
;
;
;
;
;
;
;
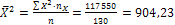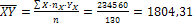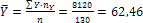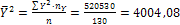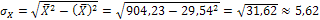Отсюда коэффициент корреляции равен:
;
Так как 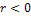, то связь обратная, то есть с ростом X убывает Y.
Так как 
, то по таблице 1 определяем, что линейная связь высокая.
Находим линейное уравнение регрессии У по X:
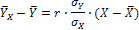
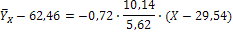
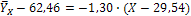
Аналогично находим линейное уравнение регрессии Х по Y:
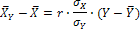
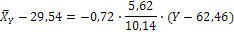
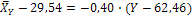
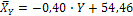
Данные уравнения устанавливает связь между признаками X и Y, и позволяют найти среднее значение признака 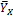для каждого значения X и аналогично среднее значение признака 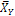для каждого значения Y.
Если линейная связь слабая, то это не исключает наличия между признаками Х и Y нелинейной (криволинейной) связи. Оценка тесноты любой связи между признаками (линейной и нелинейной) производится с помощью корреляционных отношений Y по Х и Х по Y:
; 
.
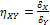Дисперсии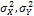 
, называемые внутригрупповыми, определены ранее. Их можно было также посчитать по формулам:
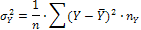
Они характеризуют разброс фактических значений от общих средних.
Все величины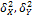 
называются межгрупповыми дисперсиями и вычисляются по формулам:
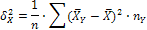
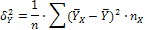
Они характеризуют разброс условных средних от общей средней. В данной задаче:
.
.
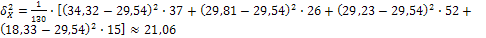Находим: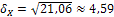 
; 
.
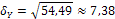Тогда корреляционные отношения равны:
Замечание. Следует отметить, что корреляционное отношение всегда принимает значение от 0 до 1, причем оно не меньше, чем коэффициент корреляции, взятый по модулю, то есть 
.
В нашем примере: 0 < 0.72 < 0.82 < 1; 0 < 0.72 < 0.72 < 1.
Ответ. Корреляционная связь между признаками высокая, ее можно описать линейными уравнениями: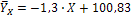 
; 
.
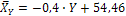