Отношение 
не определено при 
, следовательно, можно найти 
. Вычисление таких пределов носит название «раскрытие неопределенностей».
Теорема. Пусть 
и 
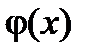непрерывны на 
и дифференцируемы внутри него, причем 
внутри отрезка и 
. Следовательно, если существует 
, то существует 
, причем
.
Доказательство. 
на , из теоремы Коши
, 
,
но по условию
.
Следовательно,
.
Если 
и 
, , 
, то 
.
.
Замечание 1. Теорема справедлива, если 
и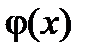 
не определены при 
, то
, 
.
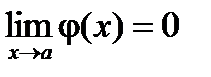Доопределяем функции и 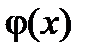в точке так, чтобы они стали непрерывными.
, 
,
так как 
не зависит от определенности в точке .
2. Если 
и производные удовлетворяют условию теоремы Лопиталя, то
.
3. Если 
, но 
, то теорема может применяться к обратному отношению
при 
при .
4. Правило Лопиталя используется, если 
, полагаем, что 
, 
, тогда
.
Можно доказать аналогичную теорему, если 
, 
.
Встречают неопределенности:
1) 
, 
;
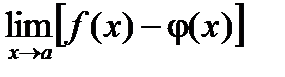2) 
, 
;
3) 
, 
;
4) 
, 
;
5) 
.
, , 
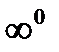приводятся к 
и 
в результате логарифмирования.
Пример 1. Вычислить 
.
Решение.
.
Пример 2. Вычислить 
.
Решение.
;
.
