Рассмотрим 
непрерывную на 
. 
достигает своего наибольшего и наименьшего значений либо на границе сегмента, либо внутри него. Если наибольшее (наименьшее) значение функции достигается во внутренней точке 
, то это значение является максимумом (минимумом) функции, так как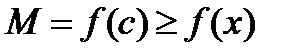 
(или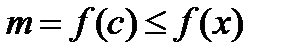 
) для любого 
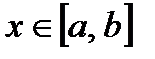, выполняется и для любой окрестности точки , лежащей внутри .
Правило нахождения наибольшего и наименьшего значений функции на сегменте :
1. Находим все критические точки в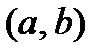 
и вычисляем в них значение функции.
2. Вычисляем 
и 
.
3. Выбираем наибольшее и наименьшее значения.
Замечание. Непрерывная на сегменте функция имеет во внутренней точке только один экстремум, то в этой точке она имеет наибольшее значение в случае максимума, и наименьшее значение, в случае минимума.
