При исследовании функции важно установить форму ее графика при неограниченном удалении точек графика от начала координат, как говорят, при удалении его переменной точки в бесконечность. Иногда график приближается к некоторой прямой.
Асимптотой графика функции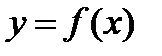 
называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю, при неограниченном удалении этой точки по графику от начала координат.
1. Асимптоты параллельны оси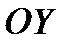 
(вертикальные). Пусть при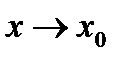 
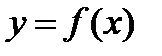неограниченно возрастает по абсолютной величине, то есть 
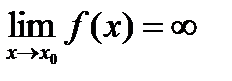. Следовательно, 
является асимптотой. Очевидно, обратное, если 
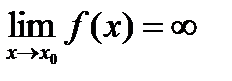является асимптотой, то , то есть для нахождения вертикальной асимптоты надо найти точки, где функция обращается в бесконечность (терпит бесконечный разрыв) (рис. 18).
|
| Рисунок 18 – |
Асимптота имеет уравнение
.
Пример. Найти вертикальные асимптоты функции 
.
Решение. 
, следовательно, 
– уравнение вертикальной асимптоты.
2. Асимптоты, не параллельные оси 
(наклонные). Пусть график функции 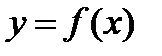имеет асимптоту, не параллельную оси 
. Следовательно, уравнение ее
(частный случай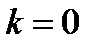 
– горизонтальная асимптота).
Для определения 
и 
поступим следующим образом (рис. 19).
|
| Рисунок 19 – |
Опустим из точки 
перпендикуляр 
на асимптоту. Из определения асимптот следует, что при 
,
.
Из треугольника 
имеем 
, так как 
, то 
одновременно с 
, то есть 
.
Так как 
, то 
.
– бесконечно малая величина.
,
, 
,
,
.
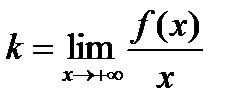Если хотя бы один из пределов не существует, то 
асимптоты не имеет.
Аналогично при 
.
