График дифференцируемой функции 
называется выпуклом в интервале 
, если он расположен ниже любой своей касательной на этом интервале (рис. 14).
|
| Рисунок 14 – |
График дифференцируемой функции называется вогнутым в интервале 
, если он расположен выше любой своей касательной на этом интервале (рис. 15).
|
| Рисунок 15 – |
График функции в одних интервалах может быть выпуклым, а в других – вогнутым.
Теорема (достаточный признак выпуклости или вогнутости). Пусть имеет 
во всех точках . Если во всех точках 
, то график функции выпуклый, если же 
, вогнутый.
Доказательство. Допустим 
, докажем, что график будет выпуклым. Возьмем на графике точку 
и проведем через 
касательную (рис. 16).
|
| Рисунок 16 – |
Для доказательства мы должны установить, что график в расположен ниже касательной, то есть для любого 
, не равного 
, принадлежащего ,
.
Уравнение касательной
.
Разность ординат касательной и графика
,
.
преобразуем по формуле Лагранжа
, 
.
.
, 
.
,
, 
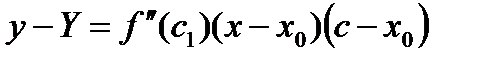(либо < 0),
.
на , следовательно, 
, 
.
Аналогично, для 
.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Пусть в точке 
непрерывна.
Теорема (достаточный признак существования точки перегиба). Если 
меняет свой знак при переходе через , то в точке с абсциссой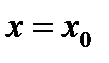 
график функции имеет точку перегиба.
Доказательство. Пусть 
при 
, 
при 
.
В этом случае, слева выпуклый, справа вогнутый, то есть точка отделяет интервал выпуклости от вогнутости, точка (, 
) является точкой перегиба (рис. 17).
|
| Рисунок 17 – |
В точке производная либо непрерывна, либо разрывна, в случае непрерывности 
, так как по условию теоремы 
при переходе меняет знак. Поэтому точку перегиба следует искать только среди точек, где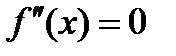 
.
