Розглянемо на координатній площині 
пряму, задану загальним рівнянням
і точку 
поза цією прямою.
Рівняння у відповідній тривимірній системі координат 
визначає площину, паралельну до осі 
з нормальним вектором 
. (Рис. 38.1).
Рис. 38.1
Проведемо 
- перпедикуляр до прямої. Тоді 
- це відстань як до прямої у системі 
, так і до площини у системі 
. Тоді за формулою після покладення 
, знаходимо 
Обчислення кута між прямими на координатній площині здійснюється в залежності від того, якими рівняннями вони задані. При задаванні прямих загальним рівнянням 
кут між прямими визначається як кут 
між їх нормальними векторами 
і 
і обчислюється за формулою аналогічно до:
У випадку завдання прямих канонічними рівняннями
кут між прямими визначається як кут 
між їх напрямними векторами 
і 
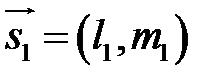і обчислюється згідно формули:
Розглянемо випадок, коли прямі задано рівняннями з кутовим коефіціентами:
Нехай 
і 
кути, утворені цими прямими з додатним напрямком осі 
(Рис. 38.2):
Рис. 38.2
Тоді за властивостю зовнішнього кута трикутника 
, або 
.
Тоді 
, або оскільки 
, 
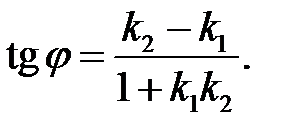
Оскільки паралельні прямі нахилені до осі 
під однаковим кутом, то умовою паралельності прямих є рівність
Якщо прямі перпендикулярні, то 
і тангенс кута 
є нескінченно великою величиною. Тому умова перпендикулярності цих прямих має вигляд:
