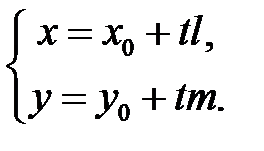Рівняння прямої у відрізках на осях.
Якщо знайти пряму, що утворюється перетином площини, заданої рівнянням у відрізках на координатних осях, і координатної площини 
, то вона визначатиметься рівнянням
Пряма, що задається рівнянням, перетинає осі 
та 
у точках 
і 
(Рис. 37.1)
Рис. 37.1
і відтинає на них відрізки довжиною 
, 
. Рівняння називається рівнянням прямої у відрізках на координатних осях.
Канонічне і параметричне рівняння прямої на площині.
Нехай є ненульовий вектор 
і точка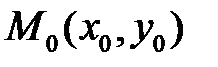 
, тоді рівняння прямої, що проходить через дану точку паралельно вектору згідно, має вигляд:
Це канонічне рівняння прямої на площині.
Параметричне рівняння отримується з відкиданням третього рівняння, яке перетворюється у тотожність вигляду 
:
