Будь яка ліня 
, що знаходиться у площині 
,може бути утворена як перетин деякої поверхні, заданої рівнянням 
, і площини 
(Рис. 36.1)
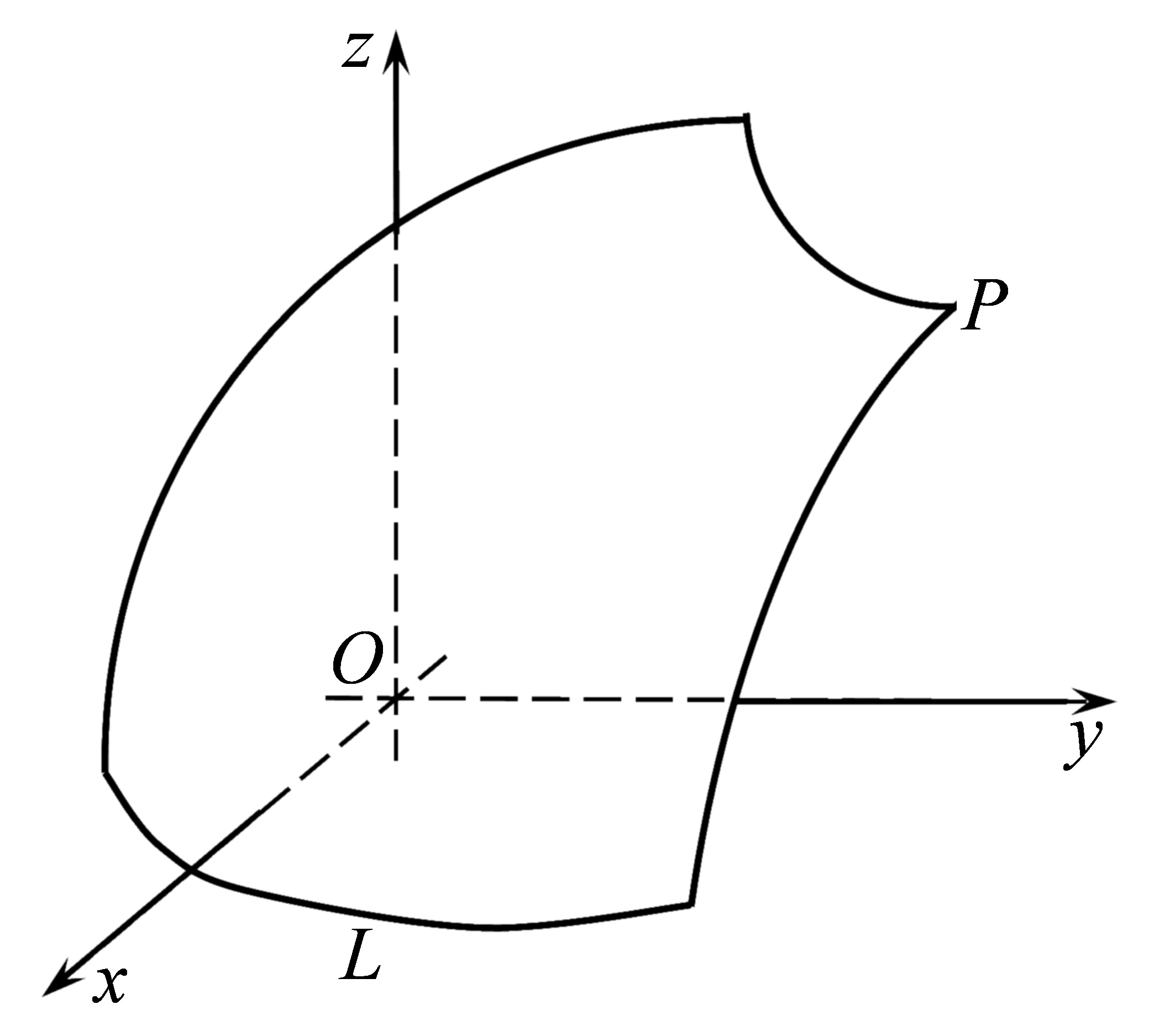
Рис. 36.1
Тоді кожна точка лінії 
задовольняє систему рівнянь
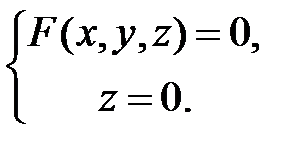
Можна у перше рівняння підставити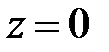 
і перепозначити 
. Тоді набуває вигляду
Це загальне рівняння лінії, що належить площині 
, записане у тривимірній системі координат 
. Якщо розглядати двовимірну систему координат 
, то загальне рівняння лінії виглядає наступним чином:
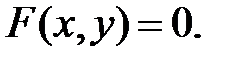
Параметричне рівняння лінії, що належить площині 
, згідно подається так:
, 
або 
, 
Отримаємо рівняння кола радіус 
, центр якого співпадає з точкою площини 
.
Для цього у тривимірній системі координат 
візьмемо сферу у цій самій точці. Вона визначається наступним рівнянням
Коло утворюється як перетин цієї сфери з площиною 
(Рис. 36.2).
Рис. 36.2
Воно визначається системою рівнянь
яка еквівалентна одному наступному рівнянню вигляду
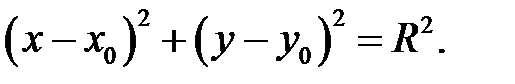
Рівняння і є рівнянням кола на координатній площині 
з центром у точці 
і радіуса 
.
Пряма на координатній площині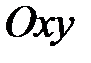 
може бути утворена перетином цієї площини з довільною площиною (Рис. 36.3), яка задана загальним рівнянням
.
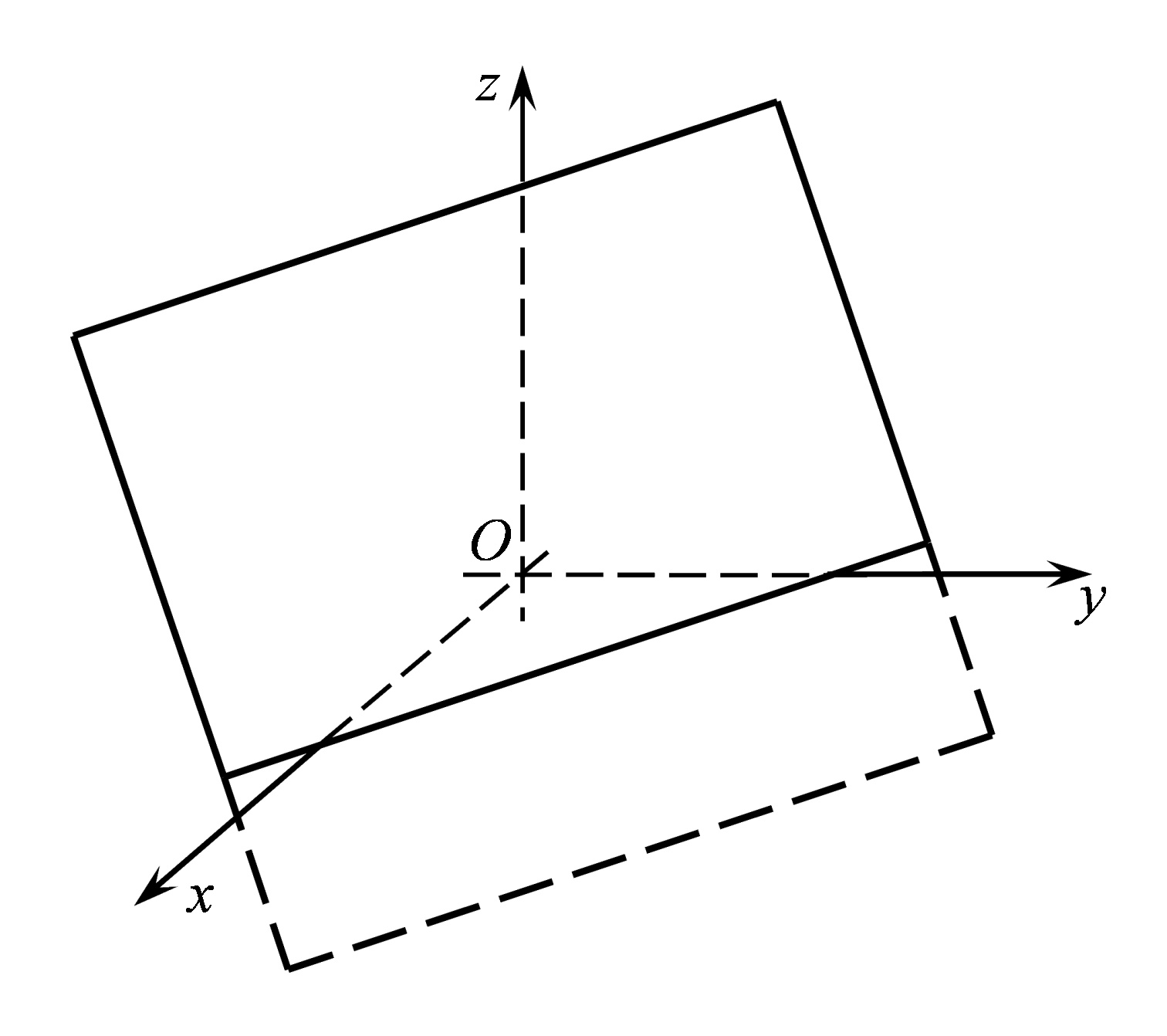
Рис. 36.3
Причому у рівнянні хоча б один з коефіцієнтів 
чи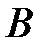 
має бути відмінним від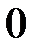 
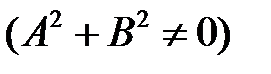. Інакше площини 
і будуть паралельними і не перетинатися. Тоді пряма, що утворюється внаслідок перетину, визначається системою рівнянь
,
або одним рівнянням: 
.
Для зручності в останньому рівнянні перепозначимо коефіцієнти і запишемо його у вигляді:
Має місце теорема:
Теорема. Будь-яке рівняння визначає на координатній площині пряму, перпендикулярну до вектора 
.
Дійсно, оскільки 
, то рівняння має хоча б один розв’язок. Нехай 
- будь-який розв’язок цього рівняння. Тоді є вірною рівність
.
Складемо різницю рівнянь і
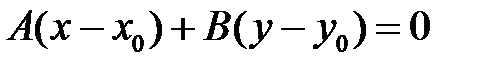
Розглянемо точки 
і вектор 
. Рівняння можна записати у вигляді 
. Це означає, що усі вектори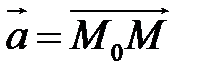 
мають початок у точці 
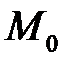і перпендикулярні до вектора 
, тобто знаходяться на одній прямій, що перпендикулярна до цього вектора. Саме цю пряму визначає рівняння.
Рівняння називається загальним рівнянням прямої на координатній площині. Якщо розглянути довільні 
і 
, то це рівняння визначає усі прямі, що проходять через точку 
і називається рівнянням пучка прямих, що проходять через задану точку.
