Зобразимо рисунок.
Рис. 39.4
Знайдемо одну точку на прямій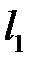 
. Для цього в її рівняння підставимо, наприклад, 
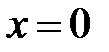. Одержимо 
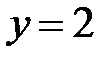, тобто точка на прямій 
. Перетворимо рівняння другої прямої, перенісши всі доданки в ліву частину рівності:
.
Відстань між двома прямими – це відстань від точки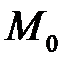 
до прямої 
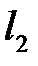. (Рис. 39.4). Відстань від точки 
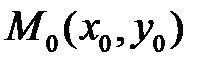до прямої 
обчислюється за формулою.
В нашому випадку
.
Задачі для самостійної роботи
1. Записати рівняння прямої з кутовим коефіцієнтом, якщо їй належать точки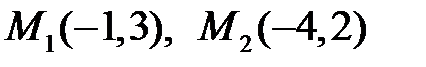 
2. Задано вершини трикутника: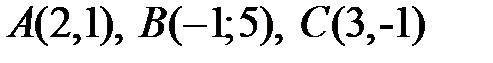 
. Знайти рівняння висоти, що проведена із вершини С.
3. Довести, що прямі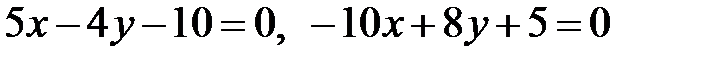 
паралельні і обчислити відстань між ними.
4. Дано точки: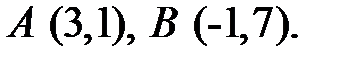 
Скласти рівняння прямої, яка проходить через середину відрізка AB перпендикулярно цьому відрізку.
5. Обчислити відстань від точки 
до прямої 
6. Визначити кут між двома прямими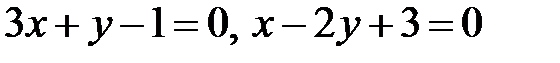 
.
7. Скласти рівняння медіани АМ трикутника з вершинами 
, 
, 
.
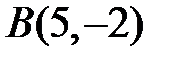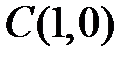8. Дано дві точки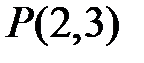 
та 
. Скласти рівняння прямої, що проходить через точку Q перпендикулярно до відрізку PQ.
9. Через точки 
та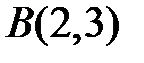 
проведено пряму. Визначити точки перетину цієї прямої з осями координат.
10. Знайти рівняння прямої, яка проходить через точку перетину прямих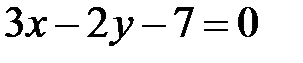 
і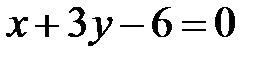 
та точку 
.
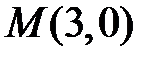11. Знайти рівняння прямої, яка проходить через точку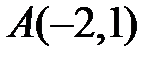 
паралельно прямій 
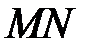, якщо 
, 
.
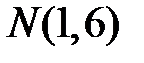12. Знайти точку, симетричну точці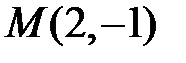 
відносно прямої 
.
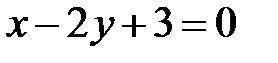13. Знайти точку 
перетину діагоналей чотирикутника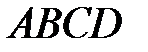 
, якщо 
, 
, 
, 
.
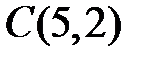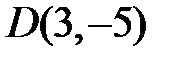14. Скласти рівняння висоти, яка проведена через вершину 
трикутника 
, якщо відомі рівняння його сторін: 
, 
, 
.
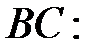
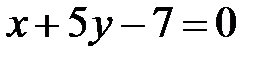15. Записати рівняння прямої, яка проходить через точку 
та утворює з віссю 
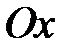кути: а) 
, б) 
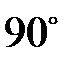, в)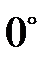 
.
16. Задано рівняння висот трикутника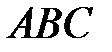 
, 
та координати його вершини 
. Знайти рівняння сторін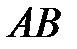 
та 
трикутника.
17. Подані рівняння двох сторін паралелограма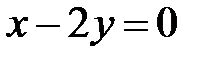 
, 
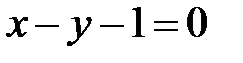та точка перетину його діагоналей 
. Знайти рівняння двох інших сторін.
Питання для повторення
1) Рівняння кола. Загальне рівняння прямої на площині.
2) Види рівнянь прямої на координатній площині.
3) Відстань від точки до прямої на площині. Кут між прямими.
