Нехай пряма, що проходить через точку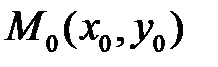 
, задана рівнянням і утворює з віссю 
кут 
(Рис. 37.2). Тоді нормальний вектор цієї прямої
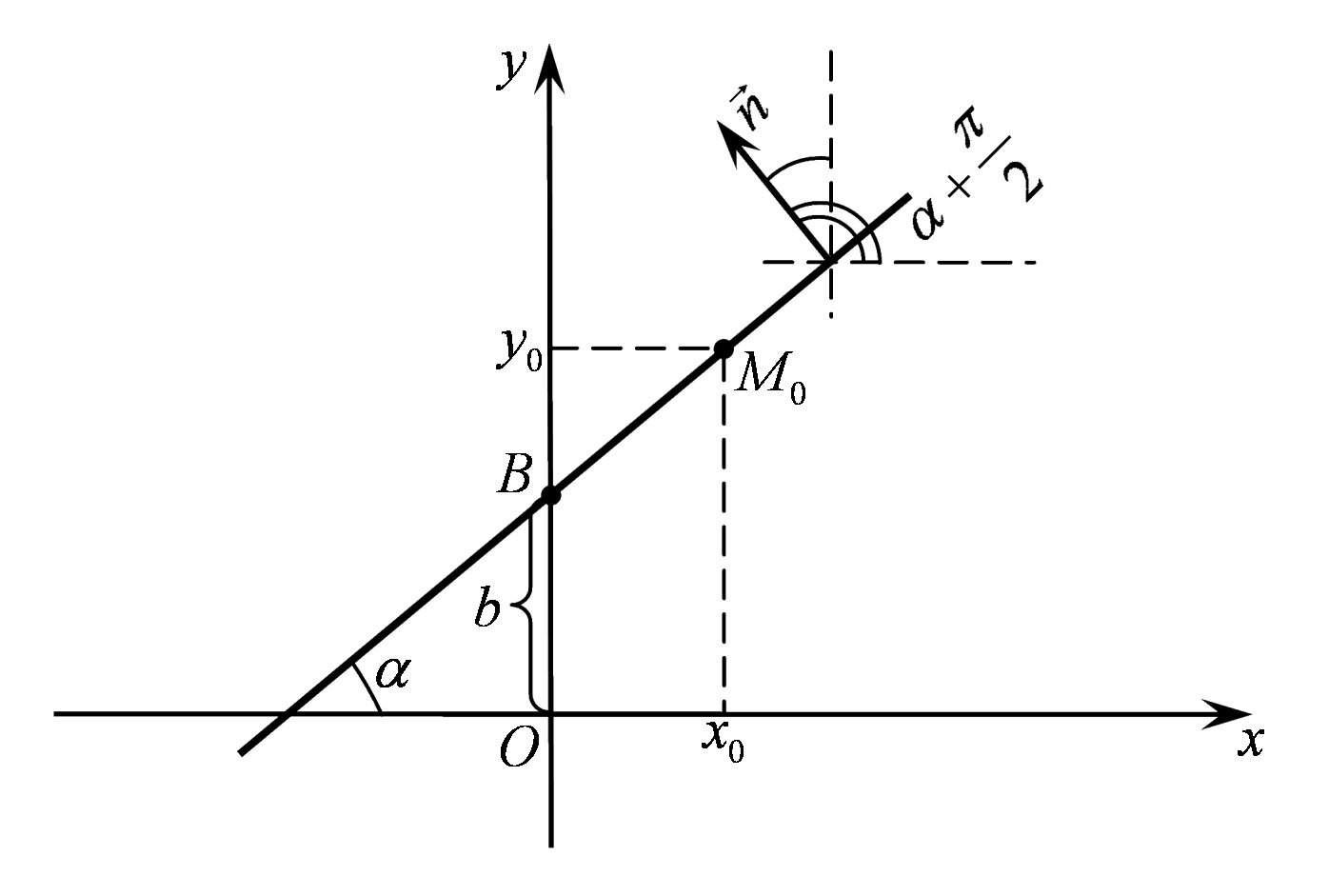
Рис. 37.2
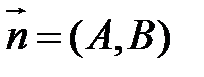утворює з осями координат кути 
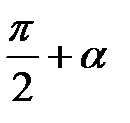і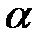 
і для його координат виконується рівність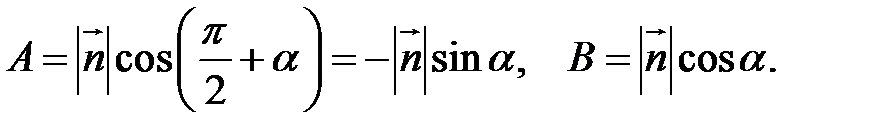 
За допомогою останніх формул з знаходимо
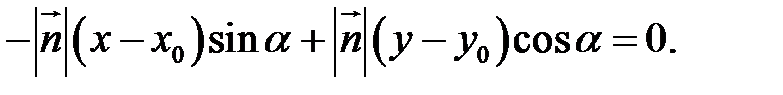
Оскільки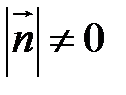 
, ділимо обидві частини на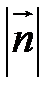 
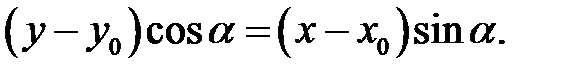
Нехай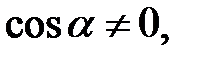 
тобто пряма не паралельна осі 
. Введемо позначення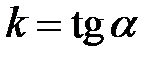 
. Тоді останнє рівняння перепишеться у вигляді
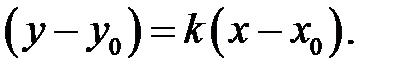
Число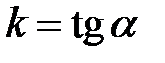 
, яке дорівнює тангенсу кута, утвореного прямою з додатним напрямом осі 
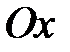, називається кутовим коефіцієнтом прямої.
Якщо вважати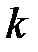 
довільним, то рівняння визначає пучок прямих, що проходять через точку 
, за виключенням прямої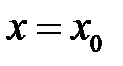 
, паралельної до осі 
.
Здійснимо за рівнянням (9.5) наступні перетворення
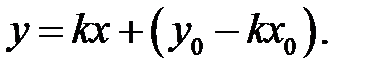
і введемо позначення 
. Знайдемо рівняння
де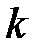 
-кутовий коефіціент прямої, 
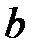- координата точки 
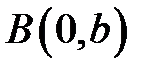перетину прямої з віссю 
. Рівняння називається рівнянням прямої з кутовим коефіціентом.
