Отношения порядка

множество, на котором задано отношение порядка, причем любые два элемента множества М сравнимы; частично упорядоченное множество - то же, но допускаются пары несравнимых элементов.

Линейно упорядоченным является множество точек на прямой с отношением "правее", множества целых, рациональных, действительных чисел по отношению "больше" и т п.

Примером частично упорядоченного множества могут служить трехмерные векторы, если порядок задан так 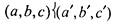, если

, т е если предшествование выполнено по всем трем координатам, векторы (2, 8, 5) и (6, 9, 10) сравнимы, а векторы (2, 8, 5) и (12, 7, 40) не сравнимы. Этот способ упорядочения можно распространить на векторы любой размерности: вектор

предшествует йектору если

и выполнено

На множестве векторов можно рассмотреть и другие примеры упорядочения.

1) частичный порядок: , если

, т.е. по длине векторов; несравнимыми являются векторы одинаковой длины.

2) линейный порядок: , если a<d\ если а -d, то b < е; если жед = с?и6 = е,то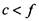

Последний пример представляет понятие алфавитного порядка.

Алфавит - это кортеж попарно различных символов, называемых буквами алфавита. Примером служит алфавит любого европейского языка, а также алфавит из 10 арабских цифр В компьютере клавиатура и некоторые вспомогательные средства определяют алфавит допустимых символов.

Слово в алфавите А - кортеж из символов алфавита А. Слово записывается символами алфавита подряд, слева направо, без пробелов Натуральное число является словом в цифровом алфавите Формула не всегда является словом из-за нелинейного расположения символов наличие надстрочных (показатели степени) и подстрочных (индексы переменных, основания логарифмов) символов, дробная черта, знаки радикалов и др.; однако путем некоторых соглашений она может быть приведена к записи в строку, что и применяется, например, в компьютерном программировании (так, знак возведения в степень записывается как 2 знака умножения подряд: 5**3 означает третью степень числа 5.

Лексико-графическое (алфавитное) упорядочение -для различных слов 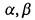в алфавите с упорядоченными

символами устанавливается упорядочение: , если

возможно представление 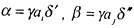, при котором либо

(подслово может быть пустым), либо 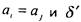- пустое подслово

В этом определении - префикс (начальное подслово), одинаковый у обоих слов - либо первые по счету слева различные

символы, либо - последний символ в слове- хвостовые

подслова.

Таким образом, алфавитное упорядочение слов определяется первым слева различающим их символом (например, слово КОНУС предшествует слову КОСИНУС, поскольку они впервые различаются в третьей букве, и Н предшествует С в русском алфавите). Считается также, что символ пробела предшествует любому символу алфавита - для случая, когда одно из слов является префиксом другого (например, КОН и КОНУС)

Упражнение. Проверьте, что алфавитное упорядочение натуральных чисел, имеющих одинаковое число разрядов в десятичной записи, совпадает с упорядочением их по величине.

Пусть А - частично упорядоченное множество. Элемент называется максимальным в А, если не существует элемента для которого а < b. Элемент а называется наибольшим в А, если для всякого отличного от а элемента 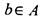выполнено Ь<а-

Симметричным образом определяются минимальный и наименьший элементы. Понятия наибольшего и максимального (соответственно, наименьшего и минимального) элементов различны -см. пример на рис.14. Множество на рис. 14,а имеет наибольший элемент р, он же является максимальным, минимальных элементов два: s и t, наименьшего нет. На рис.14,б, напротив, множество, имеющее два максимальных элемента / и j, наибольшего нет, минимальный, он же наименьший - один: т.

Вообще, если у множества есть наибольший (соответственно, наименьший) элемент, то только один (может не быть ни одного).

Максимальных и минимальных элементов может быть несколько (может не быть совсем - в бесконечном множестве; в конечном случае -обязательно есть).

Разберем еще два примера. - отношение на множестве N:

"Y делит X", или "X является делителем числа Y" (например,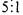

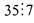) является рефлексивным и транзитивным. Рассмотрим его на конечном множестве 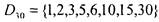делителей числа 30.

Отношение 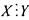является отношением частичного порядка (нестрогого)

и изображается следующей матрицей порядка 8, содержащей 31 знак

"+".

Соответствующая схема с 8 вершинами должна содержать 31 связку.. Однако она будет более удобна для обозрения, если исключить 8

связок-петель, изображающих рефлексивность отношения 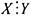(диагональные элементы матрицы) и транзитивные связки, т.е. связки

, если есть промежуточное число Z такое, что

(например, связку 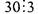, поскольку ). Тогда в схеме

останется 12 связок (рис.15); недостающие звенья подразумеваются "по транзитивности". Число 1 является наименьшим, а число 30

наибольшим элементами в . Если исключить из число 30 и

рассмотреть тот же частичный порядок на множестве , то

наибольшего элемента нет, но имеются 3 максимальных элемента: 6, 10, 15

Теперь построим такую же схему для отношения на булеане

(множестве всех подмножеств) 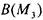трехэлементного множества

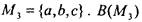содержит 8 элементов:

Проверьте, что если сопоставить элементам а,Ь,с, соответственно числа 2, 3, 5, а операции объединения множеств - умножение соответствующих чисел (т.е., например, подмножеству 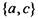отвечает

произведение 2 • 5 = 10), то матрица отношения 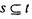будет точно такой

же, как для отношения 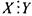; схемы этих двух отношений с описанными

сокращениями петель и транзитивных связок с точностью до обозначений совпадают (см. рис.16). Наименьшим элементом является

а наибольшим -

Бинарные отношения R на множестве А и S на множестве В называются изоморфными, если между А и В можно установить взаимно однозначное соответствие Г, при котором, если (т.е.

элементы находятся в отношении R), то 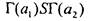(образы

этих элементов находятся в отношении S).

Так, частично упорядоченные множества и 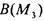изоморфны.

Рассмотренный пример допускает обобщение.

Отношение 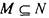на булеане 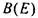есть частичный порядок. Если

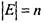, т.е. множество Е содержит п элементов , то каждому

подмножеству соответствует п -мерный вектор с

компонентами , где 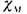- характеристическая функция

множества Л/. Совокупность всех таких векторов можно рассматривать как множество точек п -мерного арифметического пространства с координатами 0 или 1, или, по-другому, как вершины п -мерного

единичного куба, обозначаемого , т.е. куба с ребрами единичной длины. Для п = 1, 2, 3 указанные точки представляют собой соответственно концы отрезка, вершины квадрата и куба - отсюда общее название. Для /7=4 графическое изображение этого отношения - на рис.17. Около каждой вершины 4-мерного куба указано соответствующее

подмножество 4-элементного множества и четырехмерный

вектор, представляющий характеристическую функцию этого подмножества. Соединены между собой вершины, отвечающие подмножествам, которые различаются присутствием ровно одного элемента.

На рис.17 четырехмерный куб изображен так, что на одном

уровне расположены попарно не сравнимые элементы, содержащие одинаковое число единиц в записи (от 0 до 4), или, по-другому, одинаковое число элементов в представляемых подмножествах.

На рис.18а,б - другие наглядные представления 4-мерного куба;

на рис.18а ось первой переменной ОХ направлена вверх (намеренное отклонение от вертикали, чтобы не сливались различные ребра куба):

при этом 3-мерный подкуб, соответствующий X = 0 расположен ниже, а для X = 1 - выше. На рис. 186 та же ось ОХ направлена изнутри куба наружу внутренний подкуб соответствует X = О, а внешний - X = 1.

В файле материалов приведено изображение 5-мерного единичного куба (стр.134).