Соответствием G между множествами А и В называется подмножество 
. Если 
, то говорят, что b
соответствует а. Множество всех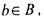 
соответствующих элементу
, называется образом элемента а. Множество всех 
которым соответствует элемент 
, называется
прообразом элемента b.
Множество пар (Ь, а) таких, что 
называется обратным по
отношению к G и обозначается 
. Понятия образа и прообраза для
' G и 
взаимно обратны.
Примеры. 1) Поставим в соответствие натуральному числу п
множество действительных чисел 
. Образом числа 5
будет полуинтервал [5, 6). Прообразом числа 5, так же как чисел 5.1,
3\/3, 5.82 является число 5.
2) Пусть, в противоположность предыдущему примеру, каждому действительному числу X поставлено в соответствие целое число [X]
(так обозначают наибольшее целое, меньшее или равное X). Прообразом числа 5 при этом соответствии является бесконечное множество: полуинтервал [5, 6).
3) Поставим в соответствие человеку его родителей. Образом при этом соответствии для каждого человека является множество из двух элементов, его мать и отец. Прообразом каждого человека Ч является множество (быть может, пустое) его детей, т.е. тех людей, для которых Ч является матерью или отцом.
Функциональное соответствие 
, или отображение -
соответствие, при котором образом любого элемента 
является
единственный элемент 
. Например, площадь геометрической
фигуры или объем пространственного тела суть их отображения в
множество неотрицательных чисел. Если А, В - числовые множества,
то соответствие 
называется функцией (хотя иногда функциями
называют и не числовые соответствия).
Упражнение. Определите, какие из соответствий трех предыдущих примеров являются функциональными.
п -местная функция (функция п переменных) -функция типа
; другая форма записи: 
, где
. Сложение, вычитание, умножение, деление, возведение в степень являются двуместными функциями. Двуместными функциями являются также тах(X, Y) \л inin(X, Y):
Функции обычно задаются вычислительными процедурами, позволяющими г,о значению аргументов определить значение функции. Примерами вычислительных процедур могут считаться формулы, графики, таблицы. В понятии формулы важным элементом является операция подстановки, или суперпозиции, позволяющая из одних функций получать другие. Разберем это понятие подробнее.
Суперпозиция функций - функция, полученная из системы
функций 
некоторой подстановкой функций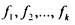 
во внешнюю функцию f вместо переменных и переименованиями переменных.
Примеры. 1) Суперпозицией внешней функции 
и функций 
является функция
или функция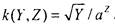 
2) Суперпозициями внешней функции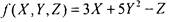 
и функций 
являются, например:
a) 
[вместо X в функцию / подставляется 
; вместо Y - функция 
b) 
[вместо X в функцию f подставляется 
; вместо У - функция
; вместо Z - суперпозиция функций
3) Класс элементарных функций есть множество всех суперпозиций так называемых основных элементарных функций (одноместных: степенных, показательных, логарифмических, тригонометрических и обратных тригонометрических) и двуместных функций, представляющих арифметические операции.
Замечание. Среди основных элементарных функций нет
двуместной функции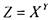 
. Ее можно выразить суперпозицией других
функций: логарифмической 
, показательной 
и
умножения в силу тождества 
Как видно из примеров, в суперпозиции функций могут измениться как сами переменные, так и их число. Заметим также, что, выполняя подстановки, мы преобразовывали формулы, выражающие функции. Формула - это выражение, описывающее суперпозицию и содержащее функциональные знаки, симзолы независимых переменных (аргументов) и констант (параметров). Формула с использованием скобок определяет порядок действий при вычислении значения функции Специальные договоренности, позволяющие упростить вид формулы, освобождают ее от некоторых скобок: так в арифметике принято, что умножение и деление связывают сильнее, чем сложение и вычитание, и одночленные сомножители не заключаются в скобки.
Суперпозицию удобно представлять в виде символической схемы
вычисления Нел и рассмотреть п -местную функцию 
как вычислительный элемент с п входами и одним выходом (см. рис.6), то суперпозиция представляет собой соединение таких элементов в схему. Определим индуктивно понятие вычислительной схемы (обратите внимание на то, как строится определение: вводятся некоторые начальные объекты, и задается способ образования из них других, более сложных объектов; такой тип определения называется индуктивным).
Пусть имеется конечное множество объектов 
, которые будем называть структурными элементами Каждый элемент имеет /;, входов и 1 выход. Графически элемент 
изображается треугольником, в
основание которого входят 
занумерованных стрелок, а из вершины
исходит одна (рис. 6а). Сеть из структурных элементов определяется следующим образом.
1) Каждый элемент 
является сетью, входы и выходы сети -соответственно, входы и выходы элемента S.
2) Пусть S - структурный элемент с т входами и 
сети из структурных элементов. Тогда соединение 
этих сетей, изображенное на рис.66, является сетью: ее входы - объединение
входов сетей 
, выходы сетей 
присоединены в
определенном порядке к элементу S в качестве входов. Заметим, что у сетей 
могут быть пересекающиеся множества входов. Выходом
сети 
считается выход элемента S
Сети 
называются подсетями, а их элементы вместе с
элементом S1 - элементами сети 
Схемой из функциональных элементов называется сеть, элементам которой приписаны (сопоставлены) функции, так что элементу
входами соответствует 
-местная функция 
Будем
говорить, что элемент S реализует функцию 
Значения
выходов одм ix элементов служат значениями аргументов для функций других элементов в соответствии со структурой схемы, причем важен
порядок аргументов Если функция 
, сопоставленная некоторому элементу S, не определена на каком-либо наборе значений своих аргументов, то не определены значения выхода S и не определены все функции элементов, на входы которых поступают значения 
Рис 7 демонстрирует разницу в реализуемых функциях при различном порядке присоединения
На рис 8 приведен пример схемы,
состоящей из 7 элементов четырех
типов 1-местная 
, 2-местные 
и 3-
местная 
Обратите
внимание, что элемент 
реализует в отличие 
от элемента 
.функцию 
от совпадающих аргументов 
В
целом схема реализует следующую суперпозицию
Разберем 
конкретные примеры
1) Пусть 
На
рис 9 изображена схема из одно- и двухвходовых элементов, реализующих
одноместные функции 
и
двуместные функции сумму, разность, произведение
Вычислительная процедура определяется, вообще говоря, неоднозначно, и зависит от того, какие функции приняты за исходные Так,
функция 
может рассматриваться как
элементарная функция (см рис 10а) как каскад
из двух 
умножений 
(см рис 106),
или как частный случай двуместной функции 
при 
(см
рис 10в) В последнем случае мы встречаемся с функцией-константой g = 3
2) Построим схему вычисления выборочного среднего 
и
выборочной дисперсии 
для статистической выборки 
объема 3 Из математической статистики известно, что
Схема вычисления - на рис.11. Строго говоря, в условии требуется построить 2 схемы: для 
. Однако вычисление М\ является
промежуточным результатом при вычислении D\; поэтому мы построили одну схему с 2 выходами, что, конечно, не вполне соответствует данному нами определению схемы из функциональных элементов.
Упражнение: начертить схемы вычисления функций примера 2а (стр.22).
Рассмотрим еще один фимер функционального соответствия. Пусть U - универсальное множество; 
- некоторое его подмножество,
В = {0,1} - множество из двух чисел 0 и 1.
Характеристическая функция множества 
отображение 
, ставящее в соответствие элементам
множества М единицу, а элементам дополнения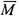 
- ноль. Легко
проверяются следующие свойства характеристической функции множеств, получаемых из множеств M,N операциями дополнения, пересечения, объединения и разности: 
;
С помощью характеристической функции удобно устанавливать некоторые соотношения между множествами.
Пример. Доказать, что 
. Обозначим 
и докажем соответствующее числовое равенство:
[поскольку А =0 или 1, то А • А = А ]=
