Алгебры

Алгебра - не только математическая дисциплина. Тот же термин обозначает вполне определенную структуру. Алгеброй называется

множество М вместе с заданной на нем системой операций

называется сигнатурой алгебры, а Л/ - носителем. Обозначение.

Примеры. 1) - алгебры на множестве

соответственно, действительных, натуральных и целых чисел с операциями сложения и умножения.

2) - множество дифференцируемых функций

действительной переменной, 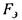элементарных функций; D - оператор

дифференцирования, ставящий в соответствие каждой функции ее производную.

Подобно изоморфизму отношений рассматривается изоморфизм

двух алгебр 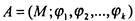и - взаимно

однозначное соответствие Г между множествами М и N и

операциями и при котором выполнено:

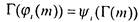для всех

Подчеркнем, что изоморфизм - это не просто взаимно однозначное соответствие (его - для конечных множеств - можно установить между любыми двумя множествами с одинаковым числом элементов) Смысл этого понятия состоит в том, что если выполнить в алгебре А какие-либо операции над определенными элементами множества М и соответствующие операции в алгебре В над соответствующими

элементами множества N, то результаты операций также будут соответствовать друг другу

Примеры. 1) Алгебры 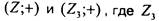- множество целых

чисел, кратных трем, изоморфны, в силу соответствия 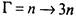. Так,

например, сложению 5 + 8=13 будет соответствовать сложение ^5 + 24 = 39, что можно проиллюстрировать схемой

2) Алгебры - множество положительных действительных чисел, изоморфны, в силу соответствия

(ввиду тождества ). Это также проиллюстрируем

схемой

В этом примере только для наглядности участвуют целые степени числа 2, чтобы их двоичные логарифмы были целыми числами.

3) Алгебры 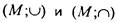на булеане 5(М) произвольного множества М изоморфны. Изоморфизм устанавливается соответствием

. В самом деле, [в силу закона

де Моргана]

Противоположный пример: алгебры 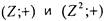, где

множество целочисленных двумерных векторов, не изоморфны. Хотя оба множества - счетны, т.е. между ними можно (многими

способами) установить взаимно-однозначное соответствие, но не удастся сделать это так, чтобы сумма векторов, поставленных в соответствие двум числам всегда соответствовала сумме этих чисел. Конечно, это требует доказательства, но мы его здесь не приводим. Особое значение имеет следующий пример. Алгебра , т.е. алгебра на булеане В(Е) с

операциями объединения, пересечения и дополнения называется алгеброй множеств на множестве Е, или алгеброй Кантора.

Частично упорядоченное множество элементов булеана В(Е) имеет наименьший элемент и наибольший Е. Для системы подмножеств множества Е выполняются свойства 1-21, приведенные в §1 главы 1.

Пример для двух- и трехэлементного множества Е фактически рассмотрен в §1 главы 1. Если трактовать операцию как сложение, операцию как умножение, а операцию дополнения А как (-А), то некоторые, но не все, из равенств 1-21 схожи с соответствующими свойствами арифметических действий над числами: 1-4 -коммутативность и ассоциативность сложения и умножения, 5 -дистрибутивность умножения относительно сложения, 7-10 и 15-18 напоминают свойства функций max и min; играет роль нуля при сложении и умножении, a U - роль единицы при умножении. Подробнее эта аналогия разбирается в гл.З.

Изоморфизм между отношением на булеане В(Е)

п -элементного множества Е и отношением делимости на множестве

О,, делителей натурального числа Н, если Я есть произведение п

различных простых чисел, можно распространить на изоморфизм между

алгебрами. Для этого достаточно определить на множестве делителей

Н операции НОК(а,Ь) - наименьшее общее кратное чисел а и Ь,

НОД(а,Ь) - наибольший общий делитель чисел а и Ъ и поставить в

соответствие простым делителям числа Я одноэлементные

подмножества множества Е (для простоты будем обозначать их теми

же символами: а,Ь,...). Тогда для соответствия (обозначаемого

символом между подмножествами Е и произведениями различных простых делителей Я выполнены соотношения:

и это соответствие есть изоморфизм.

Как видно из рассмотренных примеров, если алгебры А и В изоморфны, то элементы и операции В можно переименовать так, что В совпадет с А. Из основного равенства в определении изоморфизма следует, что любое эквивалентное соотношение в алгебре А сохраняется в каждой изоморфной ей алгебре В. Это позволяет, получив такие соотношения в алгебре А, автоматически распространить

их на все алгебры, изоморфные А. Распространенное в математике выражение "рассматривать объекты с точностью до изоморфизма" означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, т.е. являются общими для всех изоморфных объектов. В частности, изоморфизм сохраняет ассоциативность, коммутативность и дистрибутивность.

Установление изоморфизма между какими-либо системами имеет большое практическое значение. Оно сродни точному переводу на другой язык описания явлений. Когда, например, аналитическая геометрия устанавливает соотношения между геометрическими объектами - линиями или поверхностями и их аналитическими представлениями в виде уравнений, или в курсе математического анализа мы выясняем геометрический смысл производной, дифференциала или интеграла, мы получаем возможность выбирать и использовать при исследованиях и в прикладных задачах наиболее удобное для данного случая представление. В некоторых задачах изоморфизм систем служит основанием для моделирования объектов и их взаимодействия.