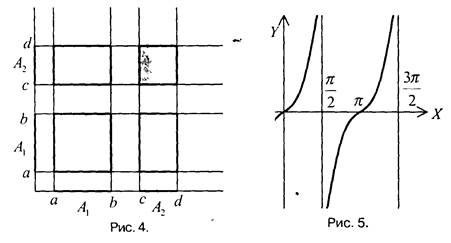
Простейший пример - задание последовательности элементов множества формулой, содержащей параметр:

Задавая различные значения параметра k, мы можем вычислять элементы множества  и т.д. Подобное задание
и т.д. Подобное задание
может быть явным, как в данном примере, или неявным, требующим разрешения. В частности, используются возвратные, или рекуррентные соотношения. Например, числа Фибоначчи задаются условиями:

Последняя формула позволяет последовательно вычислять значения

 и т.д. Возможность выразить общий n-й член этой последовательности как явную функцию параметра п для того, чтобы можно было определить, например, значение о|00, не вычисляя всех предыдущих, будет рассмотрена в разделе "Элементы комбинаторики".
и т.д. Возможность выразить общий n-й член этой последовательности как явную функцию параметра п для того, чтобы можно было определить, например, значение о|00, не вычисляя всех предыдущих, будет рассмотрена в разделе "Элементы комбинаторики".
Рассмотрим другой пример задания числового множества М порождающей процедурой:
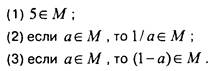
Убедимся, что множество М конечно и состоит из 6 элементов, а именно М - {5, 1/5, -4, -1/4, 4/5, 5 / 4}. В самом деле, для каждого
а, начиная со значения а - 5, есть две возможности порождения новых элементов: операциями (2) и (3). При этом могут получаться и элементы, порожденные ранее. Так, из числа 5 операцией (2) получается 1/5, операцией (3) - число (-4), а из числа 1/5 операцией (2) - снова число 5.
Рассмотрим схему порождения (рис.1), где операция (2) изображена; одинарной стрелкой, а операция (3) - двойной Схема показывает, что никаких других чисел процедуры (2) и (3) не дают.
Если же в правиле (3) заменить (1 - а) на (2 - а), то порождаемое • множество будет бесконечным: из числа 5 чередующейся t последовательностью операций (2) и (3) порождается 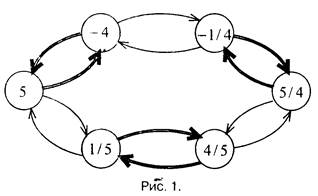
последовательность чисел

Упражнение. Проследите, какое число порождается конечной последовательностью операций 2, 3, 3, 2, 2, 3, 2, 3, 3, 2. Введем еще одно понятие.
Разбиение множества U - система непустых подмножеств
{Аи\ множества U такая, что их объединение равно U (полнота разбиения), а все попарные пересечения - пусты (чистота разбиения). Сами Аа называются классами, или блоками разбиения. Система курсов
данного факультета есть разбиение множества его студентов; система групп есть другое разбиение того же множества. Другой пример: множество всех автомобилей может быть разными способами разбито на классы в зависимости от марки, объема двигателя, компании-производителя, года выпуска, стоимости и др. При анкетировании или классификации объекты распределяются по группам; не входящие в ту или иную конкретную группу могут составлять группировку "прочие" -для полноты разбиения.
Пространство элементарных событий в некотором стохастическом эксперименте представляет собой разбиение достоверного события.
Множество прямых на плоскости разбивается на бесконечную совокупность систем прямых, параллельных тому, или иному направлению Поверхность, представляющая в трехмерной системе координат график функции двух переменных, разбивается на линии уровня.
Множество квартир дома разбивается на подмножества квартир, расположенных на одном этаже; другое разбиение - на подмножества
квартир из одного подъезда.
Если А и В - два подмножества универсального множества U, то 4 подмножества 

образуют разбиение множества V (см рис.2). Аналогично,  для 3 множеств А, В,С разбиение универсального множества U на 8 подмножеств
для 3 множеств А, В,С разбиение универсального множества U на 8 подмножеств
Л/0—Л/7 изображено на рис 3. Сами множества А,В,С могут быть представлены как объединения:

Упражнение. Выразить множества  с помощью операций
с помощью операций
 над множествами А, В, С. Указание: множество
над множествами А, В, С. Указание: множество  , например, можно представить двояко:
, например, можно представить двояко:
Каждый элемент входит  в множество в единственном экземпляре, без повторений, в отличие, например, от выборки в математической статистике. Конечная последовательность любых объектов, среди которых могут быть и повторяющиеся, называется кортежем (или вектором). Сами объекты называются компонентами кортежа. Вектором обычно называют кортеж, состоящий из чисел. Кортеж обозначается также, как вектор:
в множество в единственном экземпляре, без повторений, в отличие, например, от выборки в математической статистике. Конечная последовательность любых объектов, среди которых могут быть и повторяющиеся, называется кортежем (или вектором). Сами объекты называются компонентами кортежа. Вектором обычно называют кортеж, состоящий из чисел. Кортеж обозначается также, как вектор:  ; п называется длиной
; п называется длиной
кортежа Примером кортежа могут служить кортеж чисел, кортеж цифр в записи целого числа, кортеж букв в слове, кортеж слов во фразе.
Два кортежа считаются равными, если у них при одинаковой длине совпадают первые элементы, вторые элементы и т.д. Поэтому, например,
кортежи (7,8, А,+, 8) и (7,8,+,8, А) различны, хотя имеют одинаковый
состав.
Декартовым (прямым) произведением множеств называется
1) для двух множеств А, В. произведение Ах В - множество всех пар (а,Ь), где 
2) для п множеств  : произведение.
: произведение.  множество всех векторов
множество всех векторов  где
где 
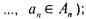 если все
если все  одинаковы и равны А, то произведение
одинаковы и равны А, то произведение 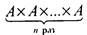 обозначается
обозначается  и называется n-й степенью
и называется n-й степенью
множества А.
Примеры. 1) Если R - множество точек числовой прямой, то  множество точек п -мерного арифметического пространства; в частности,
множество точек п -мерного арифметического пространства; в частности,
 - множество точек плоскости,
- множество точек плоскости,  - множество точек пространства трех измерений.
- множество точек пространства трех измерений.
2) Рассматриваемый в физике пространственно-временной
континуум, представляющий собой прямое произведение  , где
, где
 - трехмерное пространство, а Т - числовая ось времени.
- трехмерное пространство, а Т - числовая ось времени.
3) Географические координаты точки земной поверхности: широта
и долгота представляют элемент прямого произведения ШхД, где
Ш = [-90.+90], Д = [-\ 80,+180].
4) Известно, что прямая в трехмерном пространстве определяется двумя точками в том смысле, что через две различные точхи проходит ровно одна прямая. Упорядоченная пара точек (M,N) есть элемент
прямого произведения  , которому можно сопоставить точку 6-
, которому можно сопоставить точку 6-
мерного пространства  - 6 чисел: тройку координат точки Л/ и тройку
- 6 чисел: тройку координат точки Л/ и тройку
координат точки Л'. В этом примере пара (N,M) определяет ту же
прямую, что и (A/./V), а пара совпадающих элементов (Л/,Л/) не определяет прямой.
5) Возможные исходы при бросании игральной кости составляют множество {1,2,3,4,5,6}, т.е. отрезок [1,6] натурального ряда. Если же игральную кость бросают 4 раза, то пространство элементарных событий представляет собой [1,6], т.е. множество всех четверок  где
где 
В отдельных случаях имеют содержательный смысл не все пары, тройки и т.д. Так, в примере 3 при Ш = 90' не имеет смысла значение Д (подобно тому, как в полярных координатах при р — 0 не определено значение полярного угла <р).
Если А и В - два множества, то  ; равенство
; равенство
достигается только если  или
или  (в частности, если А- В].
(в частности, если А- В].
Практической иллюстрацией этого соотношения является следующий пример.
6} В определении возрастания функции действительной переменной на множестве фигурируют пары точек:
если 

Поэтому для функции /, возрастающей на множестве А,, выполнено условие (*) для  . Аналогично,
. Аналогично,
при возрастании той же функции на множестве  условие (*) должно выполняться для
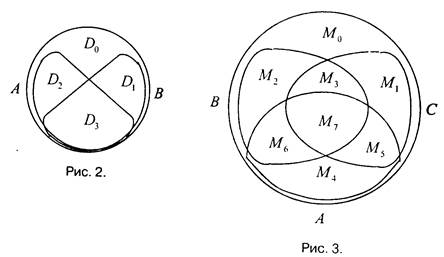
условие (*) должно выполняться для  . На рис.4 штриховкой показаны оба этих
. На рис.4 штриховкой показаны оба этих
множества, - для наглядности,  - два непересекающихся
- два непересекающихся
промежутка  . В то же время, для возрастания
. В то же время, для возрастания
функции / на объединении  необходимо, чтобы условие (*)
необходимо, чтобы условие (*)
выполнялось для любой пары 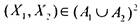 . Из рис.4 видно, что
. Из рис.4 видно, что
это множество на координатной плоскости состоит из 4 частей: двух квадратов  и двух произведений [a,b]x[c,d] и [c,f/]x[«,/>] В этих частях множества
и двух произведений [a,b]x[c,d] и [c,f/]x[«,/>] В этих частях множества  условие (*) может
условие (*) может
выполняться не для всех пар 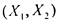 . Поэтому из возрастания функции
. Поэтому из возрастания функции
f отдельно на  и
и 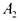 не следует, вообще говоря, возрастание на их объединении. Рассмотрите, например, функцию
не следует, вообще говоря, возрастание на их объединении. Рассмотрите, например, функцию  в областях
в областях
(0,я/2) и (я;2,Зя/2) -см рис.5.