В противополож­ность этому относительная погрешность суммы

D Z/Z = [(D X)² + (D Y)²]^1/2/(X + Y)(29)

очевидно не зависит от соотношения величин X и Y.

Следующий вывод, вытекающий из закона сложения погрешнос­тей, относится к определению погрешности среднего арифметическо­го. Мы уже говорили, что среднее арифметическое из ряда измере­ний отягчено меньшей погрешностью, чем результат каждого от­дельного измерения. Сейчас этот вывод может быть записан в количественной форме. Пусть x ₁, x ₂,..., х_n результаты отдель­ных измерений, причем каждое из них характеризуется одной и той же дисперсией S ². Образуем величину y, равную

y = (1/ n)× Ax_i = x ₁/ n + x ₂/ n +... + х_n / n.

Дисперсии этой величины S_y ² в соответствии с формулой (26) определяются как

S_y ² = S ²/ n ² + S ²/ n ² +... + S ²/ n ² = nS ²/ n ² = S ²/ n (30)

Но y, по определению, это – среднее арифметическое извсех величин x_i, и мы можем написать

S_y = S _{< x >} = S / n ^1/2. (31)

Средняя квадратическая погрешность среднего арифметического равна средней квадратической погрешности отдельного результата измерений, деленной на корень квадратный из числа измерений.

Это – фундаментальный закон возрастания точности при росте чис­ла наблюдений. Из него следует, что, желая повысить точность из­мерений в 2 раза, мы должны сделать вместо одного – четыре измерения; чтобы повысить точность в 3 раза, нужно увеличить чис­ло измерений в 9 раз, и, наконец, увеличение числа наблюдений в 100 раз приведет всего лишь к десятикратному увеличению точности измерений.

Разумеется, это рассуждение относится лишь к измерениям, при которых точность результата полностью определяется случай­ной погрешностью. В этих условиях, выбрав n достаточно большим, мы можем существенно уменьшить погрешность результата. Такой метод повышения точности сейчас широко используется, особенно при измерении слабых электрических сигналов.

Рассмотрим снова пример со взвешиванием.

Допустим, что 0.05 г – средняя квадратическая погрешность одного взвеши­ва­ния, и мы по-прежнему взвешиваем 100 образцов, кладя на весы каждый раз только один из них.

В соответствии с изложенным погрешность определения суммар­ной массы M этих образцов будет S_M = [₁S¹⁰⁰ S _i²]^1/2;.

так как погрешности всех измерений одинаковы, а всего измерений 100, то погрешность суммарной массы S_M = (100)^1/2× S = 10× S = 10´0.05 = 0.5 г.

Таким образом, мы можем утверждать, что из 1000 измерений общей массы, проделанных описанным выше способом, около 320 дадут отклонения от измеренного значения больше чем на 0.5 г, только около 50 – более чем на 1 г, и около трех – результаты которых будут на 1.5 г и более отличаться от истинного значения.

При практической работе очень важно строго разграничивать применение средней квадратической погрешности отдельного изме­рения ⁿS и средней квадра­ти­ческой погрешности среднего ариф­метического S _{< x >}.

Последняя применяется всегда, когда нам нужно оценить погреш­ность того значения, которое мы получили в результате всех про­изведенных измерений.

В тех случаях, когда мы хотим характеризовать точность при­меняемого способа измерений, следует использовать погрешность ⁿS или s, если n достаточно велико.

Поясним сказанное следующим примером.

Было сделано десять измерений электрического сопротивления провода R, в результате которых получены значения, приведенные в табл.4.

<R> = S R_i /10 = 274.7, ¹⁰S» 1.6, ⁿS _{< R >} = 1.6/10^1/2» 0.5.

Таблица 4. Измерения сопротивления

Номер измерения						б
R

Таким образом, средняя квадратическая погрешность S_R изме­рения сопротивления данного провода равна 0.5 Ом, или же, пе­реходя к относительным погрешностям, около 0.2%. Но квадрати­ческая погрешность ¹⁰ S применяемого метода измерений составляет 1.6 Ом, а относительная его погрешность – около 0.6%.

Если мы описываем метод, которым производилось измерение, то должны указать именно эту последнюю погрешность. Зная ее, можно выбрать нужное число измерений, чтобы, пользуясь табл.1V, получить желаемую случайную погрешность окончательного резуль­тата измерений.

Сейчас[9]⁾ принято среднюю квадратическую погрешность результа­та измерений записывать в скобках непосредственно после резуль­тата. В нашем примере для электрического сопротивления R это будет выглядеть так:

R = 274.7 (0.5).

 

6. СТАТИСТИЧЕСКИЕ ВЕСА

Допустим, что одним и тем же методом с одинаковой степенью точности выполнено k серий измерений. В первой серии число из­мерений n ₁, во второй - n ₂ и т.д., в k -й - n_k; если каждое измерение характеризуется погрешностью s, то погреш­ность среднего арифметического для серии с номером i будет в соответствии с формулой (26)[10]⁾

s _i = s/(n_i)^1/2.

Очевидно, что если в одной серии сделано в четыре раза боль­ше измерений, чем в другой, то погрешность результата одной серии будет соответственно в два раза меньше.

Если мы захотим для повышения точности результата усреднять его по средним значениям для обеих серий, то должны учитывать то обстоятельство, что один результат получен с вдвое меньшей погрешностью. С этой целью вводится понятие статистического веса или просто веса наблюдений. В приведенном примере за ста­тистический вес р следует принять число, пропорциональное ко­личеству наблюдений, выполненных в серии, то есть положить

p_i = k×n_i.

Подставив отсюда значение n_i в (16), имеем

p_i = k× s²/s _i ²

или, положив коэффициент пропорциональности k s² = К,получим

p_i = K/ s _i ².

Если имеется ряд результатов измерений, вообще выполненных в разных условиях, причем для каждого результата известна сред­няя квадратическая погрешность s _i, то и в этом случае можно для совместной обработки результатов приписать им соответству­ющие статистические веса p_i,положив также

p_i = B/ s _i ².

Здесь B – произвольное число. Оно обычно выбирается таким, чтобы p_i, были по возможности небольшими целыми числами. Час­то бывает, что s _i заранее неизвестны и отдельным измерениям приписываются веса на основании разного рода качественных сооб­ражений, связанных, например, с квалификацией наблюдателей, про­изводивших отдельные измерения, различием в точности измеритель­ных инструментов, с которыми они производились, и т.п.

Введение статистических весов, определенных на глаз, разумеется, нельзя считать строгим приемом, однако он дает возможность хоть как-то использовать всю совокупность наблюдений. Следует иметь в виду, что если веса отдельных наблюдений различаются в 10 и более раз (s _i и s _k различаются более чем в три раза), то обычно лучше просто отбросить из рассмотрения наблюдения с малыми весами, так как их учет может только испортить хорошие результаты.

Если нам известна совокупность ряда результатов x_i с соот­ветствующими им статистическими весами p_i, то за наивероятней­шее значение измеряемой величины следует принять уже не среднее арифметическое, а взвешенное среднее, которое также обозначим < x >:

< x > = ₁S ⁿp_ix_i /₁S ⁿp_i. (32)

Разумеется, если p ₁ = p ₂ =... = p_n, то (32) переходит в (3).

Среднюю квадратическую погрешность для < x > можно получить аналогично тому, как она была определена для равноточных изме­рений.

В результате

ⁿS _{< x >} = {[₁S ⁿpi (< x > – x_i)²]/[(n –1)×₁S ⁿpi ]}^1/2 (33)

При выборе нужного числа измерений предполагаем, что система­тическая погрешность метода достаточно мала. (Подробнее обэтом см. на стр. 67).

 

7. ОПРЕДЕЛЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА

И ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ

Ранее мы с помощью табл. II определяли доверительные вероят­ности для отдельного измерения x_i, то есть, вычисляли вероятность того, что x_i не будет уклоняться от истинного значения более чем на D x. Очевидно, важнее знать, насколько может уклоняться от истинного значения x среднее арифметическое < x > наших изме­рений. Для этого также можно воспользоваться табл.IV, взяв, однако, вместо s значение s_{< x >}, то есть s _xi / n ^1/2.

Тогда для аргумента e, с которым мы входим в табл. II, бу­дем иметь значение

e = D x /s_{< x >} = D x × n ^1/2/s. (34)

Мы теперь знаем, как определять доверительную вероятность для любого доверительного интервала, если известна средняя квад­ратическая погрешность s. Однако для того чтобы определить последнюю, нужно сделать очень много измерений, а это не всегда возможно и удобно. В тех случаях, когда измерения проводятся с помощью уже хорошо исследованного метода, погрешности которого известны, мы заранее знаем s. Как правило, однако, погрешность метода приходится определять в процессе измерений. И обычно мы можем определить только величину ⁿS, соответствующую тому или иному, но всегда сравнительно небольшому числу измерений n (² S, ³ S, ⁴ S,..., ⁿS здесь означают средние квадратические по­грешности отдельного измерения, определенные по формуле (16) для случаев двух, трех, четырех и т.д. измерений). Если для оцен­ки доверительной вероятности будем считать, что полученные нами значения совпадают с s, и воспользуемся табл.II для нахождения доверительной вероятности, то найдем неверные (завышенные) зна­чения a.

Это результат того, что при определении среднеквадратической погрешности из малого числа наблюдений мы находим эту погрешность с малой точностью. Происходящая вследствие этого неопределенность в определении погрешности приводит ктому, что когда мы заменяем s на ⁿS, то уменьшаем надежность нашей оценки, причем тем сильнее, чем меньше n.

Еще сравнительно недавно (лет 25¸30 назад) указанные обсто­ятельства не всегда принимались во внимание, да и сейчас зачас­тую не делают различия между генеральной s² и выборочной ⁿS² дисперсией.

Пусть мы определили выборочную дисперсию ⁿS ² для некото­рого числа наблюдений n и хотим определить для заданного нами доверительного интервала ±D x соответствующую ему доверитель­ную вероятность.

Очевидно, что если в формуле (34) заменим s на ⁿ S² то такому доверитель­ному интервалу будет соответствовать меньшая доверительная вероятность. Для того чтобы учесть это обстоятель­ство, интервал D x можно представить в виде

D x = t _{a, n} × ⁿS / n ^1/2, (35)

откуда

t _{a, n} = D x × n ^1/2/ ⁿS. (36)

Мы видим, что t _{a, n} – величина, аналогичная e: она играет ту же роль, но в случае, когда число измерений, из которых определе­на погрешность ⁿS,не очень велико.

Величины t _{a, n} , носящие название коэффициентов Стьюдента, вычислены по законам теории вероятностей для различных значений п и a и приведены в табл. III, также помещенной в Приложении.

Сравнивая табл.III с табл.II, легко убедиться, что при больших n значения t _{a, n} стремятся к соответствующим значениям e. Это естественно, так как с увеличением n величина ⁿS стремится к s.

Используя коэффициенты Стьюдента, мы можем переписать ра­венство (21) в виде

P ( [<x> – t _{a, n} ⁿS / n ^1/2] < x < [< x > + t _{a, n} ⁿS / n ^1/2] ) = a. (37)

Пользуясь этим соотношением и табл. III, легко определять довери­тельные интервалы и доверительные вероятности при любом неболь­шом числе измерений.

Дадим примеры применения табл. III. Пусть среднее арифмети­ческое из 5 измерений будет 31.2. Средняя квадратическая погреш­ность, определенная из 5 измерений, равна 0.24. Мы хотим найти доверительную вероятность того, что среднее арифметическое отли­чается от истинного значения не более чем на 0.2, то есть будет вы­полниться неравенство 31.0< x < 31.4,

Значение t _a,5 определим, подставив полученные результаты в формулу (36), тогда

t _a,5 = 0.25^1/2/0.24 = 1.86.

По табл. III находим для n = 5 при a = 0.8 имеем t _0.8,5 = 1.5, а при a = 0.9 имеем t _0.9,5 = 2.1.

Вообще говоря, можно обычно удовлетвориться ответом,что доверительная вероятность для этого случая лежит межу 0.8 и 0.9. Если нужно получить более точное значение, то вычислим пропорци­ональную часть подобно тому, как это обычно делается при пользо­вании таблицами.

Нужную нам величину вычисляем из пропорции

Da/(a₂ – a₁) = (t _a,n – t _{0.8, n} )/(t_0.8,n – t _0.9,n),

откуда

Da = 0.1×(0.36/0.6) = 0.06, a = a₁ +Da = 0.8 + 0.06 = 0.86.

Таким образом, доверительная вероятность получается равной 0.86.

Вычислим теперь, какова доверительная вероятность в случае 10 измерений при той же средней квадратической погрешности 0.24 и том же доверительном интервале 31.0¸31.4. По формуле (36) определяем

t _a,10 = 0.2×10^1/2/0.24» 2.6.

Из табл. III находим, что ближайшее меньшее значение

t _a,10 = 2.3 для a = 0.95

и ближайшее большее значение

t _a,10 = 2.8 для a = 0.98.

Пропорциональную часть найдём из соотношения

Da = 0.3×0.03/0.5» 0.02.

Окончательно a = 0.97.

 

 

8. СРАВНИТЕЛЬНАЯ ОЦЕНКА

РЕЗУЛЬТАТОВ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ

Пусть мы получили ряд измерений одной и той же величины. В нем всегда могут оказаться отдельные результаты, подозрительно отличающиеся (в большую или меньшую сторону) от остальных чле­нов ряда.

Следует ли их принимать во внимание при статистической обра­ботке или нужно отбросить, как явно ошибочные?

Очевидно, что нельзя пользоваться интуицией и нужно применять какие-то вероят­ностные критерии, на основании которых данное измерение призна­ется ошибочным и выбрасывается либо оставляется, как допустимое в данном ряду естественное статистическое отклонение. Не менее важные вопросы возникают при производстве нескольких рядов на­блюдений одной и той же физической величины. В результате мы получаем для каждого ряда свои значения < x > и S:

<x >₁, < x >₂,..., < x > _n и S ₁, S ₂,..., S_n.

Можно ли считать, что все эти результаты принадлежат одной и той же генеральной совокупности или разным? В первом случае их следует обрабатывать совместно и за счет этого уменьшать погреш­ность результата. Во втором – рассматривать их по отдельности – независимо друг от друга. Очевидно, что все эти вопросы имеют не достоверные, а лишь вероятные ответы. Расхождения между со­ответствующими результатами считаются значимыми, если вероят­ность того, что они случайны, превышает некоторую заданную нами величину, например 0.05, 0.01 или 0.001, называемую уровнем значимости.

Выбор того или иного уровня значимости, вообще говоря, произ­волен и зависит в первую очередь от того, насколько важны послед­ствия ошибочного выбора. Иначе говоря, что произойдет, если счи­тать два числа принадлежащими к одной совокупности, когда они принадлежат к разным и наоборот. Это решается совершенно анало­гично вопросу о том, когда можно считать вероятность того или иного события равной нулю (см. стр. 31).

Чем серьезнее последствия такой ошибки, тем при меньшем уров­не значимости нужно рассматривать сравниваемые числа как принад­лежащие разным совокупностям.

Вначале разберем вопрос о тех погрешностях, с которыми опре­деляется сама погрешность. Если мы находим S из очень боль­шого числа измерений, то получаем величину, как угодно мало от­личающуюся от своего предельного значения, но когда n невелико, то S отягчена случайными погрешностями, очевидно, тем меньши­ми, чем больше n.

Точно так же, как и для результатов измерений, существует закон распределения, дающий возможность установить доверительную вероятность того, что определенная нами из n из­мерений погрешность ⁿS будет отличаться от s на некоторое за­данное нами число.

Для определения доверитель­ного интервала, внутри которого находится s, можно воспользо­ваться приближенной формулой

s _nS» s/[2×(n – 1)]^1/2. (38)

Здесь s _пS – средняя квадрати­ческая погрешность ⁿ S, когда ⁿS вычислено из n измере­ний; вообще говоря, это выражение справедливо для n, большего 30, но в случае грубых оценок его можно использовать и для меньших n.

Из формулы (38) следует, что при n = 25 s_25S = s/7, то есть s определяется с точностью около 7. При n = 50 точность определе­ния s составляет около 10.

Более строгое рассмотрение дает возможность правильной оцен­ки доверительного интервала для s и прималом числе измере­ний.

 

Для этого мы введем величину c², которую определим сле­дующим образом:

c² = (n – 1) ⁿS ²/s².

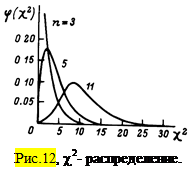
Закон распределения этой величиныизвестен под названием c²-распределе­ния, которое представ­лено графически на рис.12.

Функ­ция распределения c² характеризуется асимметричностью, осо­бенно сильной для малых n. Для больших n это распределение переходит в нормальное с дисперсией, определяемой формулой (38). Доверительный интервал для s вычисляется с помощью таблицы, составленной для нормального распределения.

При более точных оценках доверительного интервала для s мож­но воспользоваться табличными значениями, составленными для c² -распределения.

Из выражения (39) следует

s² = [(n – 1)/c²] ⁿS ² = g²× ⁿS ². (40)

Табл.III дает возможность определить значения g₁ и g₂ удов­летворяющие условию

P (g₁× ⁿ S < s) = a₁, P (g₂× ⁿS > s) = a₂.

Так как c² -распределение асимметрично, то погрешности рав­ных значений, но противоположного знака не равновероятны, как в случае нормального распределения. Отсюда следует, что при условии

a₁ = a₂×g₁ ¹ 1/g₂.