I. Типы погрешностей

 

1. СИСТЕМАТИЧЕСКИЕ ПОГРЕШНОСТИ

Погрешности измерений принято подразделять на систематичес­кие, случайные и грубые. Систематические погрешности вызывают­ся факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений, В качестве примера такой погрешности приведем взвешивание на чашечных весах с помощью моточных гирь. Если взятая нами гиря имеет погрешность, скажем, 0.1 г, то масса тела, допустим, 1000 г будет завышенной (или за­ниженной) на эту величину» и чтобы найти верное значение, необ­ходимо учесть эту погрешность, прибавив к полученной массе (или вычтя из нее) 0.1 г. Другой пример систематической погрешности приводом также из области взвешивания. Согласно закону Архиме­да, измеренный в воздухе вес тела отличается от его истинного веса на вес воздуха в объеме этого тела. Это же относится и к весу и массе гирь. Для того чтобы получить правильную массу, нуж­но после взвешивания ввести соответствующие поправки на поте­рю веса измеряемого тела и гирь. Если этого не делать, то ре­зультат взвешивания будет отягчен систематической ошибкой.

Хотя приведенные в этих двух примерах погрешности относятся к систематическим, они обладают существенным различием. Во вто­ром примере поправку на потерю веса тела в воздухе можно вычис­лить. Для этого нужно знать плотность воздуха, плотность вещест­ва, из которого сделаны гири, и плотность измеряемого тела. Эти величины обычно известны с достаточной степенью точности,

В первом примере, напротив, поправка на массу гири чаще все­го неизвестна. О ней мы знаем лишь то, что она не превышает не­которой величины (в нашем примере – 0.1 г, или 0.01%), Поэтому поправка на неточность гири не может быть учтена, и результат взвешивания мы вынуждены записать в виде

M = 1000.0, или 1000±0.1 г.

 

2. СЛУЧАЙНЫЕ ПОГРЕШНОСТИ

Если мы ничего больше не знаем о погрешности измерения мас­сы гири[2]⁾, кроме того, что она не превосходит 0.1 г. то никакие самые лучшие приемы взвешивания не позволят получить о массе тепа более точных сведений.

Однако, имея в достаточном количест­ве даже заведомо неточные гиря, можно попытаться получить луч­шие результаты.

Допустим,что мы располагаем разными наборами гирь, причем о каждом изних известно, что он выполнен с погреш­ностью, не превышающей 0.01%.

Это значит, что килограммовая ги­ря из набора имеет погрешность не более 0.1 г, стограммовая – не более 10 мг, пятидесятиграммовая – 5 мг и т.д.

Очевидно, что хотя во всех наборах гири с номинальной массой в 1 кг будут обладать погрешностью не более 0.1 г, разные экземп­ляры этих гирь характеризуются различными погрешностями. Гиря одного набора будет, например, иметь погрешность плюс 0.03 г, другого – минус 0.07 г, третьего – плюс 0.04 г и т.д.

Это происходит потому, что погрешности гирь появились в ре­зультате неточностей, имевших место при их изготовлении, которые разным образом сказались на каждой из них. Если мы произведем ряд взвешиваний, пользуясь всякий раз гирями из другого набора, то вследствие различия в погрешности каждой из гирь мы получим несколько отличающихся друг от друга значений масс взвешиваемо­го тела. Пусть этот ряд значений будет, например. 1000.23,1000.20, 1000.23, 1000.20, 1000.19, 1000.20, 1000.15, 1000.17, 1000.12, 1000.22 г.

Возьмем среднее арифметическое < x > этих значений:

 

< x > = (1/ n)₁S ⁿx_i = (x ₁ + x ₂ + x ₃ +... x_n)/ n. (3)

 

Здесь x ₁, x ₂, x ₃, ... x_n – результаты отдельных определений массы, В нашем случае < x > = 1000,19 г. Можно быть практически уверенным, что это число отличается от значения истинной массы меньше, чем на 0.1 г. Последнее следует из того, что среди ряда гирь, исполь­зованных нами при взвешивании, вероятно, были такие, у которых погрешность массы положительная (то есть их масса больше обозначен­ной на гире), но были и имеющие отрицательные погрешности. Ког­да мы брали среднее арифметическое, то положительные и отрица­тельные погрешности хотя бы частично компенсировали друг друга. В результате погрешность среднего арифметического < x >должна быть, вообще говоря, меньше, чем погрешность каждого из отдель­ных полученных нами значений массы x_i. Хотя это не исключает того, что некоторые из значений x_i могут оказаться ближе к ис­тинной массе, чем < x > – именно те значения, которые были получе­ны с наиболее точными гирями из нашего набора. Но все дело в том, что мы не знаем, какая из наших гирь более точная. Если бы это было известно, то при взвешивании просто нужно восполь­зоваться лучшими гирями и отпала бы необходимость производить взвешивание несколько раз. Мы это делаем именно потому, что не знаем погрешности каждой из гирь.

Можно полагать, что чем больше наборов таких гирь у нас име­ется, а следовательно, чем больше взвешиваний с использованием различных гирь мы сможем произвести, тем ближе к истинному будет значение, вычисленное по формуле (3), Таким образом, ре­зультаты наших отдельных взвешиваний оказыва­ются отягченными разными погрешностями для разных взвешиваний, о которых нам пока ничего неизвестно, кроме того, что любая из них не превыша­ет 0.1 г.

Среднее арифметическое значение из всех взвешиваний так­же содержит погрешность, которая, вероятно, меньше 0.1 г, но и о ней сейчас мы ничего больше не можем сказать.

Погрешности такого рода носят название случайных (потому что они отличаются друг от друга в отдельных измерениях и эти раз­личия имеют случайную, неизвестную нам величину). Правила опре­деления случайных погрешностей изучаются в теории погрешностей – математической дисциплине, основанной на законах теории вероят­ностей, В дальнейшем мы приведем некоторые положения теории погрешностей, необходимые для простейшей математической обра­ботки результатов измерений. Выводы этих положений зачастую до­вольно сложны и громоздки и здесь поэтому не приводятся.

 

3. ГРУБЫЕ ПОГРЕШНОСТИ

Третий тип погрешностей, с которыми приходится иметь дело, – грубые погрешности, или промахи. Под грубой погрешностью изме­рения понимается погрешность, существенно превышающая ожидае­мую при данных условиях. Она может быть сделана вследствие неверной записи показаний прибора, неправильно прочитанного от­счета, и т.п. В нашем примере со взвешиванием вследствие промаха могла быть записана масса 100.20 г или, например, 2020.0 г вместе 1000.20 г. При измерении длины линейкой промах может появиться в результате того, что один из концов измеряемого предмета ока­жется совмещенным не с 0 линейки, а, скажем, с делением 10 см, причем отсчет будет сделан без учета этого обстоятельства, что приведет к завышению измеряемой длины на 10 см.

 

4. ИСТОЧНИКИ ПОГРЕШНОСТЕЙ

Таким образом, мы различаем три основных типа погрешностей.

1. Систематические, значение которых одинаково во всех измерениях, проводящихся одним и тем же методом с по­мощью одних и тех же измерительных приборов.

2. Случайные. Они имеют различные значения даже для измерений, выполненных одинаковым образом. Случайные погреш­ности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. В приведен­ном выше примере источником случайных погрешностей была неоди­наковая масса гирь, но даже при взвешивании одними и теми же гирями мы, вообще говоря, будем получать разные значения веса.

Источником погрешностей может быть, например: колебание возду­ха, воздействовавшее неодинаковым образом на чашки весов; пы­линка, осевшая на одну из чашек; нагревание одной половины коро­мысла от приближения руки взвешивающего; разное трение в правом и левом подвесах чашек и множест­во других причин, которые практи­чески невозможно учесть.

3. Грубые погрешности. Источником таких по­грешностей (промахов) является недостаток внимания эксперимен­татора. Для их устранения нужно соблюдать аккуратность и тщатель­ность в работе и записях результатов. Иногда можно выявить про­мах, повторив измерение в несколько отличных условиях, например, перейдя на другой участок шкалы прибора, как это изображено на рис.1. Следует иметь в виду, что многократное измерение подряд одной и той же величины в одних и тех же условиях не всегда да­ет возможность установить грубую погрешность.

Действительно, если при измерении угла наблюдатель записал 45⁰32^'20'' вместо 35⁰32'20'', то при повторных наблюдениях он иногда будет обращать внимание только на минуты и секунды, продолжая механически за­писывать 45° вместо 35°. Для того чтобы надежно установить, при­сутствие грубой погрешности, нужно либо сместить шкалу, либо по­вторить наблюдение, спустя такое время, когда наблюдатель уже забыл полученные им цифры. Разумеется, повторение измерения дру­гим наблюдателем, который не знает результатов, полученных пер­вым, почти всегда поможет вскрыть грубую погрешность, если она имела место. Однако не следует считать и этот метод абсолютно надежным.

Если, например, погрешность произошла из-за нечетко обозначенного деления шкалы (иногда путаются цифры 5 и 6 или 3 и 8), то второй наблюдатель может повторить ошибку первого.

Далее будут указаны еще некоторые признаки, позволяющие иног­да отличить грубые погрешности от закономерных результатов на­блюдений. При всяком опыте такого рода погрешности должны быть исключены, и, как уже говорилось, основной способ их устранения – особая тщательность и внимание во время работы,

 

5. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ПОГРЕШНОСТИ

Качество результатов измерений k обычно удобно характеризовать не абсолютной величиной погрешности D x, а ее отношением к найденному значению измеряемой величины D x / x _изм, которое называют относительной погрешностью и обычно выражают в про­центах:

k = D x _отн = (D x / x _изм)´100%. (4)

[или по-нашему, по-простому: d x = D x / x _изм В. Г. ]

Величина, обратная относительной погрешности, называется точнос­тью и обозначается Q. По определению,

Q = < x >/D x. (5)

Удобство такого представления происхо­дит отчасти от того, что с отвлечен­ными числами обычно проще иметь дело, чем с именованными, но главным образом приме­нение относительной погрешности связано с тем обстоятельством, что в большинстве приложений именно эта величина играет су­щественную роль. Действительно, если мы измеряем с погрешностью около 1 см какую-либо длину, то в слу­чае, когда речь идет об определении длины карандаша, это будет очень скверная точность (около 10); если же с погрешностью до 1 см определить расстояние от Москвы до Ленинграда, тоэто будет чрезмерно высокая точность (»6×10⁷), и измерять с такой точ­ностью в данном случае очень трудно, да и нет необходимости. По­этому указание абсолютной погрешности обычно мало говорит о дей­ствительной точности, если не сопоставить ее значение со значением измеряемой величины. С этой точки зрения относительная погреш­ность всегда дает более непосредственное представление о качестве измерений.

Следует иметь в виду, что погрешность, получающаяся в процес­се измерений, вообще говоря, различна для разных значений изме­ряемой величины. Однако для погрешностей той или иной природы связи между значением погрешности и измеряемой величиной могут быть различными.

Поясним сказанное примером.

Допустим, что мы определяем дли­ну отрезка с помощью деревянной линейки длиной l, которая удли­нилась после ее изготовления и нанесения делений (например, вслед­ствие набухания); пусть удлинение всей линейки равно D l. Каж­дый сантиметр линейки оказался удлиненным на величину d l = D l / l.

Если измеряемый отрезок имеет длину А, то вследствие удлине­ния линейки его длина будет определена с погрешностью D A = A ×(D l / l). В этом случае относительная погрешность величины А остает­ся постоянной:

D A / A = d l (6)

Разберем теперь случай, когда общая длина измерительной линей­ки правильна, но каждое деление нанесено так, что погрешность в отсчете от начала шкалы до этого деления не превышает d l. Погрешность измерения длины с помощью такой линейки не будет зависеть от измеряемой длины А, следовательно относитель­ная погрешность измерения D A / A = d l / A будет обратно пропорциональна A.

Возможен случай, когда значение погрешностей периодически ме­няется с изменением измеряемой величины. Например, это будет иметь место, если измерять время с помощью секундомера, ось стрелки которого не совпадает с центром циферблата (рис.2). Из рисунка видно, что отсчеты 15 и 45 с будут правильны, отсчет 30 с завышен, а отсчет 60 с занижен.

Иное положение оси даст другие погрешности отсчета.

Возможны и более сложные зависимости погрешности от значения измеряемой величины. Чаще всего эта зависимость лежит в проме­жутке между случаями, описываемыми формулами (6) и (7). Иначе говоря, относительная погрешность измерений не остается постоян­ной, но меняется медленнее, чем это следует из формулы (7).

Если диапазон изменения измеряемой величины велик, то всегда следует изучить характер изменения погрешностей в этом диапазоне. Обычно целесообразно организовать измерение так, чтобы оставалась по возможности постоянной их относительная погрешность.

 

 

6. УЧЕТ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ

При производстве измерений одной из основных должна быть за­бота об учете и исключении систематических погрешностей, которые в ряде случаев бывают так велики, что совершенно искажают резуль­таты измерений.

Систематические погрешности можно разделить на четыре группы.

1. Погрешности, природа которых нам известна, и их значение может быть достаточно точно определено. Такие по­грешности устраняются введением соответствующих поправок.

При измерениях длины может оказаться необходимым вводить поправки, связанные, например, с температурным удлинением изме­ряемого тела и измерительной линейки; при определении веса – по­правку, вызванную "потерей веса" в воздухе, величина которой за­висит от температуры, влажности воздуха и атмосферного давления, поправку, обусловленную неравноплечностью весов, и т.д. Подобные источники погрешностей нужно тщательно анализировать, величины поправок определять и учитывать в окончательном результате. Одна­ко здесь, как и при всяких измерениях, требуется разумный подход. Поясним это на примере измерения длины. Допустим, что мы опре­деляем диаметр латунного цилиндра с помощью стальной измеритель­ной линейки, изготовленной при температуре 0°С, а измерения про­водятся при 25°С. Предположим, что измеряемый диаметр равен около 10 см, и мы хотим узнать его размер при нулевой температу­ре, Коэффициент линейного расширения латуни равен 19×10^–6 К^–1, а для стали равен 11×10^–6 К^–1.

Легко сосчитать, что при нагревании на 25° удлине­ние используемого нами участка измерительной линейки составит 0.027 мм, а увеличение диаметра цилиндра составит 0,047 мм. Разность этих величин, то есть 0.02 мм, и является поправкой наших измерений,

Обычная стальная линейка имеет миллиметровые деления. Если считать, что на глаз можно относительно уверенно отсчитать 0.2 деления, то 0.2 мм и будет той наименьшей погрешностью, которая обычно достижима с помощью такого измерительного инструмента. Примерно с такой же точностью нанесены и деления на линейке. Мы видим, что 0.02 мм, которые дает температурная поправка, на­столько меньше погрешности, вносимой самой линейкой и способом отсчета, что введение этой поправки лишено смысла.

Другое дело, если те же самые измерения производить с помощью точного из­мерительного микрометра, дающего возможность произвести измере­ния диаметра с точностью до 0.001 мм. Введение той же самой по­правки 0.02 мм при этом не только целесообразно, но и совершен­но необходимо.

Величина поправок, которые еще есть смысл вводить, разумеет­ся, устанавливается в зависимости от значения других погрешнос­тей, сопровождающих измерение. Существует правило, устанавливаю­щее, что если поправка не превышает 0.005 от средней квадратической погрешности результата измерений (см. дальше), то ею следует пренебречь. Это правило чрезмерно жесткое; обычно можно прене­бречь поправками, имеющими большее значение (что мы и рассмот­рим далее).

2. Погрешности известного проис­хождения, но неизвест­ной величины. К их числу относится уже упомянутая нами погрешность измери­тельных приборов. Она оценивается путем сравнения показаний дан­ного прибора с показаниями другого, более точного. Результат поверки приводится либо в специальном паспорте при­бора, либо указанием класса точности, который определяется ГОСТом. Класс точности электроизмерительных приборов и манометров обо­значается числом, указывающим максимальную погрешность прибора в процентах от верхнего предела измерений.

Результат поверки приводится либо в специальном паспорте при­бора, либо указанием класса точности, который определяется ГОСТом. Класс точности электроизмерительных приборов и манометров обо­значается числом, указывающим максимальную погрешность прибора в процентах от верхнего предела измерений.

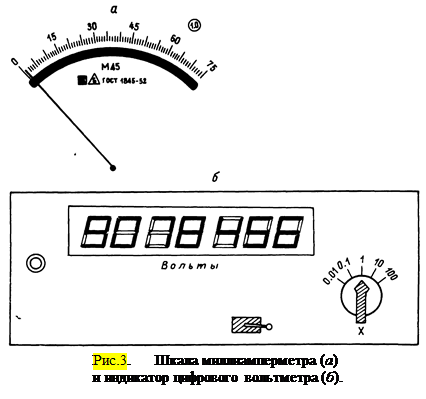
Так, миллиамперметр, шкала которого изображена на рис.3, а, дает погрешность в измере­нии силы тока не более 0.75 мА.

Очевидно, что нет никакого смыс­ла пытаться с помощью такого прибора измерять ток точнее, чем до 0.1 мА. (Если, конечно, для этого не применять каких–либо компенсационных схем, в которых наш миллиамперметр уже будет работать только как нуль-гальванометр, а не как измерительный прибор, В последнем случае погрешность измерении будет определять­ся чувствительностью миллиамперметра, которая численно равна ми­нимальному току, вызывающему заметное отклонение стрелки прибо­ра. Очевидно, что компенсационный метод измерения может снизить погрешность результата, сделав ее существенно меньшей, чем это следует из класса точности).

Широко распространенные сейчас цифровые электроизмеритель­ные приборы (см., например, рис.3, б) обычно имеют погрешность в одну – две единицы последней значащей цифры, если в паспорте при­бора не указана другая величина. Это не относится к счетчикам электроэнергии, погрешность которых существенно больше и может превышать один процент от измеряемой электроэнергии.

Класс точности весоизмерительных приборов обозначается цифрой (от 0 до 5) и буквой (а, б, в). Буква обозначает значащую цифру в числе, указывающем относительную погрешность в процентах, а цифра – место, которое она занимает после запятой. Например, класс точности 2 б соответствует допустимой погрешности 0.02%, класс 0 б – 2% и т.д. Максимальные погрешности, даваемые измерительными линейками, микрометрами и некоторыми другими приборами, либо указываются на самом приборе, или приводятся в его паспорте. Обычно дается наибольшая абсолютная погрешность, которую мы вынуждены считать постоянной по всей шкале прибора, если последний не сопровождает­ся специальной таблицей поправок для каждого деления шкалы. Та­кие таблицы прилагаются только к наиболее точным измерительным приборам.

На хороших измерительных приборах цена деления шкалы согла­сована с классом данного прибора. В таком случае нецелесообразно пытаться на глаз оценивать малые доли деления, если они не отме­чены на шкале. Однако это правило при изготовлении приборов не всегда выполняется, и иногда есть смысл оценивать по шкале чет­верть или даже одну десятую деления, но не следует особенно пола­гаться на такую оценку, тем более что при оценке на глаз 0,1 де­ления разные наблюдатели делают различную систематическую погре­шность, доходящую до 0.2 деления.

Систематические погрешности описываемой группы, вообще гово­ря, не могут быть исключены, но их наибольшее значение, как пра­вило, известно, и если мы, измеряя ток с помощью миллиамперметра (рис.3, а), получили i = 65.3 мА. то можем написать i = 65.3±0,8 мА. Здесь ±0.8 означает, что сила тока лежит где–то в пределах от 64.5 до 66.1 мА. Больше мы ничего о силе тока ска­зать не можем.

3. Погрешности, о существовании ко­торых мы не подозреваем, хотя они могут быть очень значительными. Чаще всего такие погрешности появляются при сложных измерениях, и иногда бывает, что какая-нибудь величина, которая считается опре­деленной с точностью, например, 50¸100, в действительности ока­зывается в 2 раза больше измеренного значения.

Так, например, если мы захотим измерить плотность какого–то металла и для этого определим объем и массу образца, то совершим грубую ошибку, если измеряемый образец содержал внутри пусто­ты, например, пузыри воздуха, попавшие при отливке.

Здесь приведен простейший пример, и в данном случае источник погрешности и ее размер определить не так уж трудно, хотя при очень точных измерениях плотности описанное обстоятельство может играть немаловажную роль.

При более сложных измерениях нужно всегда очень тщательно продумывать их методику, чтобы избежать больших ошибок такого рода; и чем сложнее опыт. тем больше осно­ваний думать, что какой–то источник систематических погрешностей остался неучтенным и вносит недопустимо большой вклад в погреш­ность измерений. Один из наиболее надежных способов убедиться в отсутствии таких погрешностей – провести измерения интересующей нас величины совсем другим методом и в других условиях. Совпа­дение полученных результатов служит известной, хотя, к сожалению, не абсолютной, гарантией их правильности.

Бывает, что и при изме­ре­нии разными методами резуль­таты отягчены одной и той же ус­кользнувшей от наблюдателя систематической погрешностью, и в этом случае оба совпавшие друг с другом результата ока­жутся одинаково неверными.

Вся история развития точных наук показывает, что от такого ро­да погрешностей не свободны даже самые лучшие, наиболее тщатель­но проведен­ные измерения. Они оказались присущими и основным физи­ческим константам, значения которых в последние годы были не­однократно пересмотрены.

Очень часто какая-либо величина измеряется в несколь­ких лабо­раториях одним и тем же методом с погрешностью, ска­жем, 0,01%. В то же время значе­ния, полученные в этих лабора­ториях, расходят­ся между собой иногда на 0.1% или даже более. Поэтому возникло поня­тие меж­лабораторной погреш­ности, ко­торая характеризует такие расхо­ждения.

Разумеется, тщательный анализ условий опыта иногда по­зволяет устано­вить причину рас­хождения и прийти к согласован­ному значе­нию. Однако часто это бывает совсем не просто.

В качестве иллюстраций приведем диаграммы, показы­вающие, как менялись случай­ные погрешности измерений и численные значе­ния некоторых основных физических констант за период с 1952 по 1973 г. (рис.4)[3]⁾.

У каждой точки, дающей относительное отклонение от ныне принятого значения кон­станты (точки на оси абсцисс), по вертикали отложены относи­тельные значения случайных погрешнос­тей (см. с. 36). Мы видим, что расхождение между значениями, по­лученными в разное время, иногда сущест­венно превышает величи­ну слу­чайных погрешностей. Это оз­начает, что, по крайней мере, некоторые результаты измерений содержат наряду со случайной и систематическую погрешность, ответственную за наблюдаемые рас­хо­ждения.

4. Погрешности, об­у­слов­ленные объ­ектом измерений. Эта группа, хотя и не связана не­посредственно с измерительными операциями, может существенным образом искажать результат измерений.

Поясним сказанное на примере измерения площади сечения ци­линдра, который мы считаем круговым, но в действительности он имеет овальное сечение.

Если будем измерять диаметр AB (рис.5), то получим большие значения, чем при измерении диаметра A'B'. Измерив ряд диаметров и взяв среднее из полученных значений, можно определить число, лучше характеризующее размер цилиндра. Если же измерять только один диаметр и считать цилиндр круглым, то вычисленное по этим измерениям значение будет содержать сис­тематическую погрешность, определяемую степенью овальности ци­линдра и выбранным для измерения диаметром.

Однако если при измерении диаметра цилиндра в нескольких на­правлениях получается одинаковый результат, мы еще не можем быть уверенными в том, что цилиндр круглый.

Действительно, про­ведем три окружности, радиусы которых равны стороне равносторон­него треугольника, а центры находятся в его вершинах. Фигура, ограниченная дугами этих окружностей и вершинами треугольников (рис.6), обладает тем очевидным свойством, что при измерении ее размеров штангенциркулем в любом направлении мы будем по­лучать одно и то же значение, равное длине стороны треугольника a.

Рассчитанная по этим значениям площадь «круга»» будет p×a²/4. В действительности легко показать, что площадь этой фигуры будет (a²/2)×(p–3^1/2). Отношение измеренной и действительной пло­щадей составит 1.16, то есть будет допущена погрешность около 15%. Этот пример представляется очень любопытным и наглядно показы­вающим, насколько осторожным нужно быть в выборе метода изме­рений для исключения систематической погрешности. Цилиндр, имею­щий в сечении фигуру рис.6, является удивительным примером «не­круглого катка», с помощью которого можно с успехом перекатывать грузы, как по круглому (рис.7). Существуют и другие фигуры, об­ладающие указанным свойством.

Приведем еще пример. Если для измерения электропроводности металла взят отрезок проволоки из этого металла, имеющий какой-либо дефект, например утолщение, трещину, неоднородность.

Со­противление такого куска будет неверно характеризовать электро­проводность материала. Происходящая из-за этого погрешность является систематической.

Однако, как мы видели на примере взвешивания с помощью не­верной гири, систематическая погрешность в ряде случаев может быть переведена в случайную. В примере с гирями для этого было необходимо провести несколько взвешиваний, пользуясь для каждого из них гирями из другого набора.

Точно так же систематическая погрешность, связанная со свой­ствами измеряемого объекта, часто может быть переведена в слу­чайную.

В наших примерах для этого нужно: в первом – измерить ряд диаметров цилиндра и взять среднее значение, во втором – из­мерить сопротивление нескольких отрезков проволоки и взять сред­нее. Впрочем, как было только что показано, этот прием может и не дать требуемых результатов, ибо не всякий способ усреднения автоматически приводит к исключению систематической погрешнос­ти» Действительно, например, присут­ст­вующие часто в металле га­зовые пузырьки всегда снижают его плотность.

При измерении плот­ности разных образцов, взятых из одной и той же отливки, будем иметь несколько отличные значения вследствие неравномерного рас­пределения газовых включений в отливке. Но все полученные значе­ния плотности будут ниже истинной и произведенное таким образом усреднение не может привести к исключению систематической по­грешности, обусловленной присутст­вующим внутри металла газом. Все же в большом числе случаев перевод систематических по­грешностей в случайные оказывается полезным, помогая улучшить точность получаемых результатов.

Из изложенного можно сделать чересчур пессимистический вы­вод о том, что поскольку численное значение и природа системати­ческих погрешностей нам почти никогда неизвестны и их существо­вание зачастую не может быть установлено, то и результаты измерений всегда могут быть отягчены погрешностью, о которой ничего сказать нельзя, кроме того, что она может иметь место. Такая точка зрения ставит под сомнение любой результат измерений.

К счастью, опыт показывает, что в действительности дело об­стоит далеко не так плохо. Если мы и не знаем точного значения систематических погрешностей, то все же внимательный анализ ус­ловий эксперимента обычно позволяет установить достаточно надежно, по крайней мере, верхнюю их границу, и измеренные нами вели­чины определяется с точностью, заслуживающей доверия и непрерыв­но улучшающейся с ростом техники измерений. Систематическая погрешность, призрак которой всегда преследует экспериментатора, является некоторым стимулом совершенствования техники измере­ний и, в конце концов, не мешает получению данных, успешно ис­пользуемых во всех областях науки и техники. Это является лучшей гарантией того, что в подавляющем большинстве измерений систе­матические погрешности могут быть определены и учтены достаточ­но хорошо. Хотя, разумеется, от них полностью не застраховано ни одно самое лучшее измерение.

Итак, допустим, что все систематические погрешности у нас учтены, то есть поправки, которые следовало определить, вычислены, класс точности измерительного прибора известен и есть достаточная уверенность, что отсутствуют какие-либо существенные и неизвест­ные нам источники систематических погрешностей.

В этом случае результаты измерений все же несвободны от слу­чайных погрешностей, правила вычисления которых даны ниже.

Ес­ли случайная погрешность окажется меньше систематической, то очевидно, что нет смысла пытаться еще уменьшить величину случай­ной погрешности, все равно результаты измерений не станут от этого заметно лучше, и, желая получить большую точность, нужно искать пути к уменьшению систематической погрешности. Наоборот, если случайная погрешность больше систематической, то именно случайную погрешность нужно уменьшать в первую очередь.

Мы уже говорили, что если произвести ряд измерений и взять среднее арифметическое из него, то случайная погрешность этого среднего будет меньше, чем погрешность единичного измерения.

Для уменьшения случайной погрешности следует произвести не одно, а ряд измерений, причем, как мы увидим дальше, тем больший, чем меньшую величину случайной погрешности мыхотим получить. Од­нако очевидно, что нет смысла производить измерений больше, чем это необходимо, чтобы систематическая погрешность существенно превышала случайную,

 

Отсюда вытекают правила, которые будут далее сформулированы более точно.

1. Если систематическая погрешность является определяющей, то есть она существенно больше случайной погрешности, присущей дан­ному методу, то достаточно выполнить измерение один раз,

2. Если случайная погрешность является определяющей, то изме­рение следует производить несколько раз. Число измерений целесо­образно выбирать таким, чтобы случайная погрешность среднего арифметического была меньше систематической погрешности, с тем, чтобы последняя опять определяла окончательную погрешность ре­зультата.

Однако следует иметь в виду, что мы можем ограничиться одним измерением лишь в тех случаях, когда из других источников нам из­вестно, что случайная погрешность меньше, чем систематическая.

Это обычно имеет место при измерениях известным методом, погрешности которого в какой–то степени изучены. Так, например, если определить длину карандаша с помощью измерительной линей­ки с погрешностью делений в 1 мм, то можно быть уверенным, что случайная погрешность много меньше 1 мм, и следует ограничить­ся одним измерением. Точно так же мы знаем, что случайная по­грешность взвешивания на обычных торговых весах меньше 5 г, в то время как цена деления шкалы таких весов 5 г и присущая им систематическая погрешность близка к этому значению. Следова­тельно, надо взвешивать на таких весах не более одного раза, что обычно и делается. Наоборот, при взвешивании на некоторых моделях точных лабораторных весов случайная погрешность взвешивания боль­ше систематической, и для повышения точности часто производят несколько взвешиваний.

Таким образом, необходимое число измерений определяется в конечном итоге соотношением значений систематической и случай­ной погрешностей. Количественное уточнение этого правила будет приведено дальше, после того как мы познакомимся с элементами теории вероятностей, знание которых нужно для количественных оценок случайных погрешностей.

 

7. СВЯЗЬ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

Выше указывалось, что можно перевести систематическую по­грешность в случайную, организовав измерения таким образом, что постоянный фактор, влияющий на результат измерений, в каждом из них действует разным образом, то есть результат его действия но­сит случайный характер.

Этот прием превращения систематической погрешности в случай­ную называется рандомизацией. Он позволяет практически исклю­чить многие неизвестные систематические погрешности. Приведем еще два примера такого исключения систематических погрешностей.

Если мы для определения урожайности поля соберем урожай с какого-либо его участка, а затем помножим результат на отноше­ние площадей поля и контрольного участка, то полученный таким образом общий урожай может быть искажен систематической погреш­ностью, связанной с тем, что плодородность почвы на поле меня­ется от одного его края к другому.

Чтобы этого избежать, можно разбить поле на ряд малых квадратов одинаковой площади, перену­меровать их и отобрать для измерения ряд участков случайным образом, например, записав номера участков на бумажках, вытяги­ватьих, как в лотерее. Так мы переведем систематическую по­грешность, обусловленную различием в урожайности разных частей поля, в случайную.

Другой пример: измеряется удлинение стержня под действием растяжения. Если мы знаем изменение длины и упругих свойств стержня в зависимости от температуры, то, делая измерения при разных температурах, будем вносить соответствующую поправку.

Однако вместо этого можно, не зная зависимости свойств стержня от температуры, произвести ряд измерений растяжения при разных случайно выбранных температурах.

Погрешность, происходящая вследствие изменения температуры, будет случайной, а конечный результат – соответствовать удлине­нию стержня при средней температуре.

Разумеется, такого рода исключение систематических погреш­ностей практически далеко не всегда возможно. Поэтому разделение всех погрешностей на систематические и случайные целесообразно.

 

8. ПОГРЕШНОСТИ ПЕРВОГО И ВТОРОГО РОДА

В тех случаях, когда измеряются какие-то характеристики го­товой продукции – диаметр подшипника, состав металла и т.п. – задача измерений обычно состоит не в получении точного значения измеряемой величины, а в необходимости уложиться в определен­ные допуски, установленные для данной продукции.

Те изделия, ко­торые не соответствуют этим требованиям, будем называть браком. Но следствием погрешностей измерений могут быть два обстоятель­ства:

1) хорошее изделие бракуется или

2) брак пропускается.

Поясним это примером. Диаметр вала равен 60 мм с допуском 0.013 мм. При измерении диаметра мы получили число 60.012 мм. Погрешность нашего измерительного устройства составляет 0.002 мм. Следовательно, мы признаем вал годным, хотя на самом деле он мог иметь диаметр 60.014 мм, то есть должен считаться браком. В этом случае мы совершили погрешность второго рода.

Наоборот, если при той же точности измерений оказалось, что диаметр вала 60.014 мм, то мы его забракуем, хотя в действительности его раз­меры могут находиться внутри допуска (скажем, составлять 60.012 мм). В этом случае сделана погрешность первого рода.

Очевидно, что когда размеры изделия находятся вблизи границ допуска, всег­да есть вероятность сделать погрешность первого или второго ро­да. Казалось бы, что наиболее страшна погрешность второго рода – пропуск брака. Это действительно так, когда мы имеем дело с очень дорогими и ответственными изделиями. В таком случае иног­да лучше забраковать 100 хороших изделий, чем пропустить одно бракованное. Однако для менее ответственных изделий чересчур жесткий контроль, необходимый для полного отсутствия погрешнос­тей второго рода, нецелесообразен. Действительно, чем вернее хо­тим мы застраховать себя от погрешностей второго рода, тем больше (при неизменной точности измерений) делаем погрешностей первого рода. Разумеется, невыгодно и нецелесообразно переводить в брак сотню хороших шариковых ручек, чтобы не пропустить в партии одной плохой. Такой излишне строгий контроль будет неоправданно уве­личивать стоимость изделий. Выбор экономически целесообразной сис­темы измерений и браковки во всех случаях очень важен.

 

II НЕКОТОРЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

И СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И СЛУЧАЙНЫЕ СОБЫТИЯ

Мы уже знаем, что большинству измерений сопутствуют случай­ные погрешности, отличающиеся тем, что при каждом повторном измерении они принимают другое, заранее не предсказуемое зна­чение. Существует еще много величин, обладающих тем свойством, что их точное значение не может быть указано и меняется от опы­та к опыту. Такого рода величины называют случайными. Но не следует думать, что о численном значении случайных величин вооб­ще ничего нельзя сказать. Как правило, можно указать границы, в которых оно находится, а также установить, насколько часто внут­ри этого интервала интересующая нас случайная величина принима­ет то или, иное значение. Опыт обычно показывает, что в разных случаях некоторые из этих значений появляются более часто, а другие – реже. Совокупность наблюденных значений такой величины и частоты появления каждого из этих значений позволяет устано­вить так называемый закон распределения случайной величины, ко­торый является столь же определенной ее характеристикой, как по­стоянное числовое значение, – характеристикой неслучайной величины.

Приведем примеры некоторых неслучайных и случайных величин. Моменты начала и конца солнечного затмения могут быть достаточ­но точно вычислены, и, таким образом, они неслучайны. Также не­случайно время прибытия поезда на станцию, потому что поезд дви­жется по расписанию[4]⁾. Однако момент прихода такси на стоянку уже относится к случайным величинам, так как он заранее не пре­допределен.

Более внимательное рассмотрение показывает, что разница меж­ду этими двумя классами величин не всегда может быть совершен­но четко отмечена.

Действительно, время прихода поезда на станцию приводится в часах и минутах. И не случайно "Красная стрела" прибывает в Москву в 8 ч 25 мин. Но если более точно проследить за останов­кой поезда, то мы сразу же убедимся, что каждый день это проис­ходит в разные моменты: сегодня, например, в 8 ч 24 мин 33 с, вчера – в 8 ч 25 мин 2 с и т.д. Поэтому время прихода „Красной стрелы”, измеренное с точностью до секунды, – величина случайная. То же время, измеренное с точностью до минуты, – неслучайно.

Точно так же и момент солнечного затмения, вычисленный на основании законов движения тел Солнечной системы, известных с некоторой точностью. Она и задает точность определения времени начала и конца затмения. В этом смысле момент начала затмения не относится к случайным величинам. Однако в пределах интерва­ла времени, меньшего, чем тот, который может быть получен на основании наших знаний о движении Земли и Луны, момент наступ­ления затмения должен рассматриваться как случайный.

Итак, числовые величины, характеризующие то или иное собы­тие, часто являются случайными.

Наряду с этим сами события в одних и тех же условиях опыта могут произойти или не произойти.

Если подбросить монетку, то она может упасть либо гербом, либо противоположной стороной. Для хорошей монеты (не погнутой с ровными краями и т.п.) выпадение герба или "решки" будет в среднем происходить почти одинаково часто. Мы говорим, что оба события, то и другое – случайные, происходящие с равной вероятностью.

Рассмотрим другой характерный пример случайного события. До­пустим, имеется урна, о которой известно, что в ней содержатся одинаковые по массе и размеру шары двух цветов – черные и бе­лые. Так как шары ничем, кроме цвета, не отличаются, то, если не смотреть в урну, мы не знаем, какой шар вытащим. Возьмем из урны шар, отметим его цвет и опустим назад в урну. После пе­ремешивания повторим эту операцию снова и снова некоторое, до­статочно большое число раз.

Если в урне n белых и n черных шаров, то в среднем мы должны вытащить их примерно одинаковое число. Иначе это можно выразить так: всего в урне 2 n шаров, из них n белых. Отноше­ние числа белых шаров к общему числу шаров в урне опре­де­ляет так называемую вероятность появления белого шара. В данном случае эта вероятность будет n /2 n = 1/2. Такова же вероят­ность появления черного шаря. Если число шаров неодинаково – допустим, белых в два раза больше, чем черных, – то легко сооб­разить, что вероятность вытянуть белый шар будет равна 2/3, а черный – 1/3. Очевидно, что если, кроме белых и черных, урна других шаров не содержит, то вероятность вытянуть белый или черный шар равна 1 (1/2 + 1/2 в первом случае, 2/3 + 1/3 – во втором),

Пусть в урне содержатся шары более чем двух цветов, скажем, белые, черные и красные, соответственно в количествах n, l, и k. Условно назовем появление белого шара благоприятным событием, а появление черного или красного – неблагоприят­ным[5]⁾. Вероятностью благоприятного события будем называть отноше­ние возмож­ного числа всех благоприятных событий (оно в нашем случае определяется числом белых шаров в урне) к общему числу всех возможных событий, которые задаются количеством всех ша­ров в урне, равным n + l + m. Положив n + k = m, можем записать

P (n) = n /(n + m), (8)

P (n) будем называть вероятностью благоприятного события. Точно так же вероятность неблагоприятного события будет

P (m) = m /(n + m) (9)

Из формул (8) и (9) легко получить

P (n) + P (m) = 1. (10)

Вычислить вероятности событий можно лишь в том случае, ког­да известно, сколько событий какого типа возможно. В приведен­ном примере с урной нужно знать число содержащихся в ней бе­лых (n) и число черных и красных (m) шаров. Часто мы этого не знаем и решаем обратную задачу – по частоте появления шаров того или иного цвета в описанном выше опыте определяем вероят­ность появления белого, черного или красного. Пусть мы продела­ли N испытаний, то есть N раз доставали шар из урны, каждый раз записывали его цвет и возвращали обратно в урну. Пусть при этом мы K раз вытащили белый шар, тогда K / N называется частотой появления белого шара. Основной закон теории вероятнос­тей – закон больших чисел – утверждает, что при достаточно боль­шом числе испытаний N частота появления события (с вероятнос­тью, близкой к достоверности) как угодно мало отличается от вероятности этого события, иначе говоря, если

P (m) = m /(n + m)

(причем n и m нам неизвестны), то всегда можно выбрать до­статочно большое N, чтобы выполнялось соотношение

|P (m) – K / N| < e, (11)

где e – как угодно малое положительное число, отличное от нуля.

В принципе это соотношение дает возможность устанавливать опыт­ным путем, с какой угодно большой точностью, вероятность неиз­вестного нам случайного события.

В действительности разность P (m) – K / N убывает с увеличением N очень медленно: для того чтобы увеличить точность приближенного равенства P (m)» K / N в n раз, число испытаний надо увеличить в n ² раз, другими словами, погрешность приближенного определения вероятности обратно пропорциональна квадратному корню из общего числа испытаний. Далее будет показано, что погрешность измерения какого-либо величины при многократных измерениях также умень­шается пропорционально 1/ n ^1/2, где n – число единичных измерений.

В отличие от неслучайных событий, о которых нам может быть точно известно, появятся они или не появятся, мы никогда не мо­жем сказать этого о событиях случайных. Частота появления слу­чайного события определяется его вероятностью. Однако вероят­ностная оценка может быть достаточно падежной, и мы можем опираться на нее даже при предсказании самых важных для нас событий часто не менее уверенно, чем тогда, когда имеем дело с достоверными сведениями о событиях. Допустим, например, что у кого-то имеется билет лотереи, в которой на каж­дые 10 билетов приходится один выигрыш. Вероят­ность выигрыша для каждого би­лета составляет 0.1, тогда вероятность того, что он не выиграет, равна соответственно 0.9.

Естественно, что владелец этого билета не будет особенно удив­лен ни выигрышем, ни проигрышем. Допустим, однако, что у него есть 50 таких билетов. Какова вероятность того, что он получит хотя бы один выигрыш? В теории вероятностей доказывается, что вероятность того, что совместно произойдут несколько собы­тий, случающихся независимо друг от друга, равна произведению вероятностей каждого из них. В данном случае вероятность того, что не выиграет первый из имеющихся 50 билетов, равна 0.9; вероятность того, что не выиграет второй из них[6]⁾ – также 0.9. Тогда вероятность того, что не выиграют ни первый, ни второй, ни третий билеты, – (0.9)³, а вероятность, что ни один из 50 биле­тов не выиграет, – (0.9)⁵⁰ то есть приблизительно 0.005.

С другой стороны, вероятность того, что выиграют все 50 би­летов, будет еще гораздо меньше – (0.1)⁵⁰. Это означает, что и тот и другой случай практически никогда не осуществляется. Скорее всего, из 50 выиграют 5 билетов, но выигрыш 4 или 6 билетов будет также довольно вероятен. Менее вероятен будет выигрыш 3 или 7¸8 билетов. Теория вероятностей дает возможность подсчи­тать вероятность каждого из этих событий. Результаты расчетов сведены в табл.1.

Таблица 1.

Вероятности лотерейных выигрышей (вероятность выигрыша n билетов из имеющихся 50, если вероятность выигрыша для одного билета составляет 0,1)

n	P(n)	n	P(n)
	0.0052		0.1077
	0.0290		0.0643
	0.0779		0.0334
	0.1387		0.0191
	0.1809
	0.1850	P (0) + P (1).....+ P (10)	0.9953
	0.1541	P (11) + P (12).....+ P (50)	0.0047

 

Других событий, кроме приведенных в этой таблице, произойти не может. Такая система событий называется полной.

Резонно поставить вопрос: какой должна быть вероятность со­бытия, чтобы его наступление можно было считать достоверным? Разумеется, ответ на этот вопрос носит в значительной мере субъ­ективный характер и зависит главным образом от степени важности ожидаемого события. Поясним это двумя примерами.

Известно, что около 5% назначенных концертов отменяется. Не­смотря на это, мы все же, взяв билет, обычно идем на концерт, будучи в общем уверены, что он состоится, хотя вероятность этого всего 0.95. Однако если бы в 5% полетов терпели аварию пасса­жирские самолеты, вряд ли мы стали бы пользоваться воздушным транспортом. Для того чтобы в условиях мирного времени без осо­бой необходимости рисковать жизнью, по–видимому, нужно, чтобы вероятность смертельного исхода была бы не более 0.0001. Впро­чем, различные люди, конечно, по-разному относятся к риску, но и самые осторожные легко пойдут на него при вероятности неблаго­приятного исхода 10^–6 или 10^–7. Приблизительно такова обычно вероятность оказаться жертвой транспортной катастрофы на улице большого города, но никто из-за этого не боится выходить из дома.

Таким образом, можно назвать практически достоверными собы­тия, вероятность которых отличается от единицы на 10^–6¸10^–7, а практически невозможными те» вероятность которых меньше 10^–6¸10^–7.

Однако при достаточно большом числе испытаний эти последние события все же реализуются, и, хотя для каждого человека вероятность попасть сегодня под автомобиль меньше 10^–6, в многомиллионном городе эти события, к сожалению, ежедневно происходят.

Тем не менее, можно указать события, вероятность которых столь мала, что они вообще никогда в мире не происходили и, ви­димо, не произойдут. Можно оценить эту вероятность исходя из возраста вселенной Т и минимального промежутка времени t, который можно определить как время отдельного элементарного акта. Если принять в соответствии с современными космологиче­скими представлениями T» 10¹⁰ лет и t» 10^–30 с, то всего за время T прошло около 10⁴⁷ таких элементарных промежутков времени.

Учитывая размеры нашей галактики (R» 10²² см) и наименьшую мыслимую по современным представлениям длину (l» 10^–30 см), получаем, что галактика содержит не более 10¹⁵⁰ элементарных объемов vt.

Поэтому общее число элементарных событий за все время существования галактики не превышает 10²⁰⁰; эта оценка очень груба. Однако вероятность того, что обезьяна, без руководства ударяя пальцами по клавиатуре пишущей машинки, напишет заданное осмысленное произведение, скажем, „Незнакомку” Блока – как показывает простой расчет, составляет примерно 10^–2600. Это число настолько меньше числа 10^–200, определяющего вероятность появления одного элементарного акта, что события такого рода, как чудо Джинса – замерзание воды в чайнике на горячей плите (событие с точки зрения кинетической теории возможное, хотя и маловероятное), также как и чудо пе­чатающей обезьяны, нужно признать не просто маловероятными, но невозможными.

С другой стороны, события, вероятность которых отличается от единицы на 10^–8¸10^–10, следует всегда считать практически до­стоверными.

 

2. ВЕРОЯТНОСТНЫЕ ОЦЕНКИ ПОГРЕШНОСТЕЙ

При измерениях физических величин в тех случаях, когда основную роль играют случайные погрешности, все оценки точности из­мерения можно сделать только с некоторой вероятностью.

Действительно, случайные погрешности образуются в результате совокуп­ности ряда мелких неучитываемых причин, каждая из которых вно­сит незначительный вклад в общую погрешность. Следует считать, что часть из этих погрешностей положительна, часть – отрицательна. Общая погрешность, которая образуется в результате сложения таких элементарных погрешностей, может иметь различные значе­ния, но каждому из них будет соответствовать, вообще говоря, равная вероятность.

Поясним сказанное следующим рассуждением. Допустим, нам нужно взвесить сотню образцов, и мы располагаем весами, позволяю­щими определить массу с погрешностью 0.05 г (например, вслед­ствие того, что самая мелкая гиря, употребляемая при взвешивании, – 0.1 г). Предельная нагрузка, допускаемая весами, не позволяет класть на чашку более одного взвешиваемого образца. Спрашивается: какую погрешность мы можем допустить при определении сум­марной массы всех 100 предметов?

Мы знаем, что при каждом взвешивании погрешность может быть как положительной, так и отрицательной, не превышая в обо­их случаях 0.05 г. Естественно считать, что мы будем ошибаться одинаково часто как в сторону завышения, так и в сторону заниже­ния массы, т.е. мы можем положить вероятность получить погреш­ность +0.05, равной вероятности получения погрешности –0.05. Тогда P (+0.05) = P (–0.05) = 1/2.

При этом мы считаем, что все отдельные погрешности отлича­ются только знаком и имеют по абсолютной величине максимально возможное значение 0.05, Такое допущение только завысит общую погрешность результата, что для нас сейчас несущественно. Пусть при измерении первого образца мы допустили погрешность, равную +0.05, вероятность чего, как уже говорилось, равна 1/2. Вероят­ность того, что и при измерении второго образца мы сделаем снова положительную погрешность, будет в соответствии с известным нам правилом умножения вероятностей равна (1/2), то есть 1/4. Наконец вероятность при всех 100 измерениях сделать ошибку одного и того же знака будет (0.5), или примерно 2×10^–30. Такая ве­роятность (в соответствии со сказанным выше) с любой практиче­ской точки зрения равна нулю. Таким образом, мы пришли к заклю­чению, что невозможно сделать погрешность в общей массе образ­цов в 5 г (0.05´100), ибо вероятность такой погрешности не­значимо мало превышает нуль. Иначе говоря, действительная по­грешность при таком способе взвешивания будет всегда меньше 5 г. Мы выбрали наиболее неблагоприятный случай – погрешность каждого взвешивания имеет наибольшее значение, и все погрешности оказались одного знака.

Теория вероятностей дает возможность оценить, какова будет вероятность появления погрешностей других численных значений. Для этого введем сперва понятие средней квадратической, а также средней арифметической погрешностей.

 

3. КЛАССИФИКАЦИЯ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ И ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ПОГРЕШНОСТЕЙ

Для того чтобы выявить случайную погрешность измерений, не­обходимо повторить измерение несколько раз. Если каждое измере­ние дает заметно отличные от других результаты, мы имеем дело с ситуацией, когда случайная погрешность играет существенную роль.

За наиболее вероятное значение измеряемой величины обычно принимают ее среднее арифметическое значение, вычисленное из всего ряда измеренных значений.

Пока мы не будем задаваться вопросом о том, сколько измере­ний нужно проделать. Допустим, что сделано n измерений. Разу­меется, все они выполнены одним и тем же методом и с одинако­вой степенью тщательности. Такие измерения называются равно­точными.

Пусть минимальный интервал значений измеряемой величины, через который ведутся отсчеты, будет d x. Среднее ее значение равно < x >. Вся совокупность измерений может быть представлена в виде

k ₁ x; k ₂(<x > + d x);... k_n (< x > + n d x); k '_n(x – d x);... k ' _m (< x > – m d x).

Здесь k_i, k'_l целые числа, показывающие, сколько раз во всем ряду измерений наблюдались соответствующие значения измеряемой ве­личины (S k_i + S k ' _l = n).

Отложив по оси абсцисс величину погрешностей D x = m d x, а по оси ординат значения k, получим ступенчатую кривую, на­зываемую гистограммой. Пример гистограммы приведен на рис.8. Если увеличивать число наблюдений N, а интервал d x устре­мить к нулю, то гистограмма переходит в пределе в непрерывную кривую (изображенную на рисунке пунктиром), которая носит на­звание кривой распределения погрешностей. Обычно принимается, что погрешности подчиняются нормальному закону распределения. Описывающая его знаменитая формула Гаусса может быть выведе­на из следующих предположений.

1. Погрешности измерений могут прини­мать непрерывный ряд значений,

2. При большом числе наблюдений погреш­ности равных значений, но разных знаков встречаются почти одинаково часто.

3. Частота появления погрешностей уменьшается с увеличением значения погрешностей. Иначе говоря, большие погрешности наблю­даются реже, чем малые.

Эти довольно естественные на первый взгляд предположения приводят к закону распределения погрешностей, описываемому сле­дующей функцией:

y = [1 / (s²2p)^1/2]×exp[–(D x)²/2s²], (12)

где s² – дисперсия измерений (см. ниже), [9].

Отметим, что при выводе формулы Гаусса (12) делается ряд допущений, кото­рые не удается достаточно строго обосновать, кро­ме того, и условия 1¸3, в предположении которых она выводилась, никогда не выполняются совершенно строго. Это, например, следует хотя бы из того, что ошибки никогда не могут быть как угодно малыми.

Скажем, при измерении длины ограничением всегда явля­ются атомные размеры (»10^–8 см), при измерении электрического заряда – заряд элек­трона e (1.60 ×10^–19 Кл) и т.д.

Форма кривых Гаусса представлена на рис.9 для трех значений s, равных 1, 1/2 и 1/4. С помощью этих кривых можно установить, насколькочасто должны появляться погрешности того или иного численного значения.

Формула Гаусса подвергалась неоднократным эксперименталь­ным проверкам, которые пока­зали, что по крайней мере в той области, где погрешности измерений не слишком велики, она часто находится в отлич­ном согласии с экспериментом.

В ряде случаев экспери­менталь­ные данные лучше описываются другими функци­ями. Тем не менее, обычно поль­зуются нормальным законом рас­пределения, предполагая его справедливость само собой разумею­щейся. В действительности дело обстоит сложнее. По поводу этого закона было достаточно точно, хотя и не без сарказма, сказано, что "эксперимента­торы верят в него, полагаясь на доказательства математиков, а математики, – пола­гаясь на экспериментальное обоснование" [17, 22]. О нестрогости математического вывода мы уже говорили.

Что же касается экспериментальных обоснований, то они ничего не дают, кроме гистограммы, и всегда можно подо­брать достаточно хорошую интерполирующую функцию, от которой, разумеется, точки гистограммы (даже если она очень детально построена) будут всегда отступать в силу случайного характера погрешностей измерений.

Однако в пользу применения нормального распределения имеют­ся очень серьезные основания. Его особое значение связано со следующими обстоятельствами: в тех частых случаях, когда сум­марная погрешность появляется в результате совместного действия ряда причин, каждая из которых вносит малую долю в общую по­грешность, по какому бы закону ни были распределены погрешнос­ти, вызываемые каждой из причин, результат их суммарного дей­ствия приведет к гауссовому распределению погрешностей. Эта за­кономерность является следствием так называемой центральной предельной теоремы Ляпунова,

Основное условие ее применимости – отсутствие отдельных ис­точников доминирующих погрешностей. Для иллюстрации приведем табл.2, в которой представлены результаты обработки Бесселем погрешностей измерения угла прямого восхождения.

Таблица 2. Распределение погрешностей при измерении угла прямого восхождения (Общее число наблюдений 470, средняя квадратическая погрешность s = 0.40")

Пределы погрешностей, ('')	Число наблюдений с данной погрешностью
полученное в опыте	вычисленное по формуле Гаусса
0.0–0.1		92.3
0.1–0.2		86.5
0.2–0.3		76.7
0.3–0.4		64.0
0.4–0.5		49.8
0.5–0.6		36.7
0.6–0.7		25.4
0.7–0.8		16.9
0.8–0.9
0.9–1		6.1
Более 1		6.1

Как видим, совпадение наблюденного и рассчитанного чисел погрешностей очень хорошее, если отбросить последнюю строку таблицы, где по формуле Гаусса должно быть 6.1, а в опыте наблюдается 9.

Полу­ченное расхождение для случая D х >> 1 '' не должно нас удивлять. Ведь формула Гаусса всегда хорошо проверяется и вычисляются ее параметры только для малых D x. Распространение ее в сторону больших значений погрешностей, то есть в область, где иногда наблюдается появление всего одного – двух значений измеряемой величины, является грубой экстраполяцией, от которой ждать хороших резуль­татов не следует [7] ⁾.

Нужно также иметь в виду, что при наблюдении небольшого чис­ла случайных событий относительное уклонение частоты появления события от его вероятности может быть очень большое, так что расхождение в 1.5 раза (9 и 6) достаточно вероятно.

Следует отметить, что часто при нормальном распределении по­грешностей прямых измерений, погрешности основанных на них кос­венных измерений могут быть распределены по закону, отличному от нормального. Пусть, например, определяются диаметры шариков подшипника, погрешности измерения которых распределены по нормальному закону. Следовательно, кривая распределения симметрич­на относительно среднего значения диаметра d (рис.10,а).

Легко показать, что кривая распределения погрешностей масс ша­риков будет асимметрична относительно среднего значения массы (рис. 10,6). Это следует из того, что массы шариков m равны r× d ³p/6 (здесь r – плотность металла).

Отсюда следует, что если |s _d | = |–s _d |, то |s _m | > |–s _m |.

Разумеется, точно так же погрешности момента инерции шариков или площадей их главного сечения будут распределены по закону, который в принципе отличен от нормального. Таким образом, наря­ду с нормальным законом распределения погрешностей иногда встре­чаются и другие распределения. Так, возможен случай, когда равно­вероятно появление ошибки любой величины внутри некоторого ин­тервала, а за его пределами вероятность появления погрешностей равна нулю.

Примером такого распределения служит, скажем, измерение мас­сы с помощью точных весов и разновеса, не имеющего мелких гирь. Если у нас самая мелкая гирька 0.1 г и мы убедились, что масса тела больше 1.2 г, но меньше 1.3 г, то вс