При решении многих задач часто приходится сталкиваться с последовательностями, заданными рекуррентно, но, в отличии от последовательности Фибоначчи, не всегда возможно получить её аналитическое задание.
В 1973 году в США был издан «Справочник числовой последовательности» А. Слоуна. В нём описано более 2300 целочисленных числовых последовательностей, каждая из которых имеет свой номер.
Рассмотрим числовую последовательность:
1; 2; 5; 14; 42; 132; 429; …, имеющую в справочнике номер 577.
Члены этой последовательности названы числами Каталана. Они не так хорошо известны, как числа Фибоначчи, но имеют особенность также появляться в различных задачах, особенно в комбинаторных. В 1971 году математик Генри Гулд опубликовал библиографию на применение чисел Каталана в 243 случаях. Во многих из них известнейшие математики и не подозревали, что имеют дело с этими числами.
Первым с числами Каталана столкнулся Леонард Эйлер. Он подсчитал, сколькими способами выпуклый многоугольник может быть разделён на треугольники непересекающимися диагоналями.
В качестве примера можно привести способы разбиения на треугольники следующих фигур: квадрата, пятиугольника и шестиугольника.
Заметим, что в каждом из случаев¸ независимо от количества сторон n- угольника, число диагоналей равно (n – 3), а число треугольников (n – 2).
Число различных комбинаций указанного вида для каждого из многоугольников есть первые четыре члена (если начинать с треугольника) последовательности Каталана.
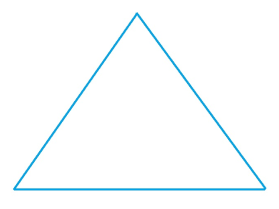


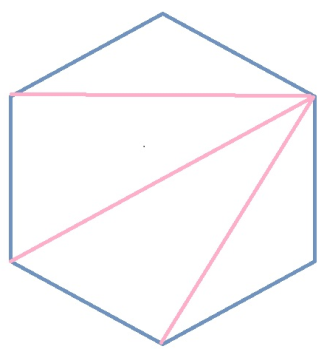





1 2 5 14
и т. д.
Эйлер, используя метод математической индукции, который, по его словам, здесь оказался трудоёмким, получил такую формулу:

Очень простые рекуррентные формулы получаются, если поместить в начале последовательности ещё одну единицу.
Пусть k – последнее вычисленное число Каталана, а n – номер следующего числа.
Тогда это число вычисляется по формуле:  .
.
Современник Эйлера, Иоганн Андрес фон Сегнер, получил загадочную рекуррентную формулу для последовательности Каталана вида: 1; 1; 2; 5; …
Запишем в ряд все уже найденные числа Каталана, а под ними запишем те же числа в обратном порядке. Умножим каждое верхнее число на соответствующее нижнее и сложим получившиеся произведения; результат и будет следующим числом Каталана.
1 1 2 5 14
*
14 5 2 1 1
14 + 5 + 4 +5 +14 = 42
Теперь вернёмся к задаче о разбиении многоугольников. Эта задача изоморфна и задачам, казалось бы с ней. Эта задача изоморфна и задачам, казалось бы с ней не связанным.
Сам Ижен Шарль Каталан, бельгийский математик, в 1838 г. решил следующую задачу: «Пусть имеется цепочка из n букв, расположенных в заданном порядке. Необходимо расставить (n – 1) пару скобок так, чтобы внутри каждой пары стояло ровно два «выражения». Этими спаренными выражениями могут быть либо две соседние буквы, либо два соседних выражения. Сколькими способами могут быть поставлены скобки?»
Для букв a и b имеется только одна возможность: (ab).
Для трёх букв таких возможностей две: ((ab) c) (a (bc)).
Для четырёх букв количество способов увеличится до пяти:
((ab)(cd)) (((ab) c) d) (a (bc) d) ((a (bc) d).
Эти числа 1; 2; 5 – первые числа Каталана, оказывается, числа Каталана дают нам количество способов расстановки скобок в буквенных цепочках соответствующих длин.
В 1961 г. Фордер, описывая числа Каталана, указал простой способ взятого однозначного соответствия между подсчётом комбинаций в многоугольниках и расстановкой скобок в буквенных цепочках.
Рассмотрим, например, семиугольник:

Обозначение основания идёт последним и обозначение для него однозначно определяется триангуляцией («триангуляция» - разбиение на треугольники). Если применить указанный приём для выше перечисленных многоугольников, то получим цепочки букв с расставленными скобками.
Английский математик Артур Кэли доказал, что числа Каталана перечисляют все плоские корневые кубические деревья (именно, n – е число Каталана равно количеству плоских корневых кубических деревьев с (n + 1) - ой концевой вершиной).
Дерево – это связный граф (вершины, соединённые отрезками), не имеющий циклов.
«Плоский» означает, что граф нарисован на плоскости без пересечений.
«Корневое» - это дерево имеет ствол, конец которого имеет корень.
Таким образом, граф можно нарисовать в виде как бы растущего вверх из земли дерева.
«Кубическое» означает, что в каждой вершине (кроме корня и концов веток) дерево разветвляется, образуя точки, в которых встречаются три ребра.

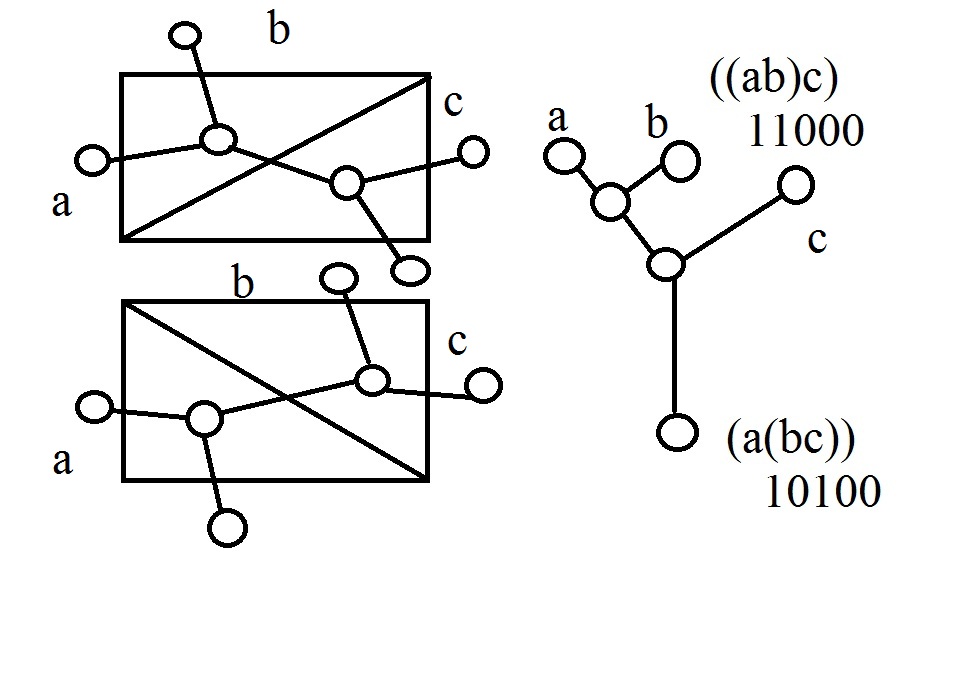
Под каждой цепочкой букв со скобками записано двоичное число, получаемое заменой всех скобок «1», а всех букв – «0», пропуская правые скобки. Для правых скобок нет необходимости вводить обозначение, т. к. заданное положение левых скобок и метод группировки букв определяет постановку скобок единственным образом.
Рассмотрим ещё такую задачу:
«Возьмём шахматные доски со сторонами 2; 3; 4; …, в которых закрашены все квадраты северо-западнее главной диагонали. Требуется провести ладью из левого нижнего угла в правый верхний. Двигаться можно, не заходя при этом на закрашенные клетки. Сколько существует путей ладьи на доске со стороной а?»
Решение:








Под стороной длины n напишем двоичное число, соответствующее корневому дереву (кубическому) с n концевыми вершинами.
Продвигаясь по двоичным разрядам числа слева на право будем двигать ладью вправо, проходя «1», и вверх, проходя «0» (последняя двоичная цифра не учитывается). Эта последовательность двоичных цифр определяет путь, и все пути ладьи могут быть получены таким образом.
Заключение
В работе на примере двух наиболее широко известных возвратных последовательностей были рассмотрены способы задания рекуррентных последовательностей, их некоторые свойства, применение в различных разделах математики.
Все поставленные в данном исследовании цели были достигнуты: сделан исторический экскурс по теории вопроса, рассмотрены различные формулы и их выводы, показано применение изучаемых в работе объектов на примере различных задач. Все рассмотренные задачи сопровождаются подробными пояснениями, доказательствами и иллюстрациями.
При работе над данной темой были использованы разнообразные источники информации такие как: печатные и электронные издания, энциклопедическая и учебная литература.
Выбранная тема зачастую остаётся за страницами школьного учебника, хотя она очень интересна и многогранна. В работе показана связь таких разделов математики как: математический анализ и геометрия, комбинаторика и теория чисел.
Эта работа позволяет более детально подойти к вопросу изучения возвратных последовательностей, полученные результаты рекомендуется рассмотреть на занятиях математического кружка.
Список литературы
1. Виленкин Н. Я. Комбинаторика. М.: Наука, 1969
2. ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ. М.: Наука, 1978
· выпуск 1. А. И. М а р к у ш е в и ч. Возвратные последовательности.
· выпуск 6. Н. Н. Воробьев. Числа Фибоначчи.
· выпуск 21. Л. И. Головин, И. М. Яглом. Индукция в геометрии.
· выпуск 11. Я. С. Дубнов. Ошибки в геометрических доказательствах.
· выпуск 32. Е. С. В е н т ц е л ь. Элементы теории игр.
Электронные источники:
http://ru.wikipedia.org/wiki/Числа_Фибоначчи
www.math.ru
www.sciteclibrary.ru






