Последовательность Фибоначчи обладает рядом свойств.
Выведем выражение этих чисел через 
. Для этого установим связь между числами данной последовательности и следующей комбинаторной задачей.
«Найти число n – последовательностей, состоящих из нулей и единиц, в которых никакие две единицы не идут подряд».
Чтобы установить эту связь вспомним задачу о кроликах, с которой мы начали наше знакомство с последовательностью чисел Фибоначчи; сопоставим последовательности, о которой идёт речь в условии, пару кроликов по правилу: единицам соответствуют месяцы появления на свет одной из пар «предков» данной пары (включая и исходную), а нулями – все остальные месяцы. Например, последовательность 010010100010 устанавливает такую «генеалогию» - сама пара появилась в конце 11-го месяца, а её родители – в конце 7-го, «дед» - в конце 5-го, а «прадед» - в конце второго. Исходная пара кроликов зашифровывается при этом последовательностью 000000000000.
Ясно, что при этом ни в одной последовательности не могут стоять две единицы подряд – только что появившаяся пара не может, по условию, принести приплод в следующем месяце. Кроме того, при указанном правиле различным последовательностям отвечают различные пары кроликов, и обратно, две различные пары кроликов имеют разную «генеалогию», так как, каждый раз пара кроликов даёт приплод, состоящий также из одной пары.
Установленная связь показывает, что число n –последовательностей, обладающих указанным свойством, равно F(n).
Докажем теперь, что
F(n) =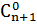 
+ 
+ 
+ …+ 
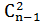, где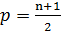 
, если n нечётно, и 
, если n чётно, иными словами 
.
Есть такая комбинаторная задача о лестнице: «Сколькими способами можно расставить n нулей и k единиц так, чтобы никакие две единицы не стояли рядом». Решение этой задачи можно изобразить в виде лестницы, причём нуль означает место, где ломаная идёт вправо, а единица – место, где она идёт вверх (как показано на рисунке). При этом, так как ступенек двойной высоты на лестнице нет, в последовательности не могут идти две единицы подряд. Таким образом, число последовательностей из n нулей и k единиц будет равно числу лестниц, т. е. 
. Число же таких последовательностей, в которые входит ровно k единиц и n – k нулей, равно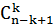 
. Так как при этом должно выполнятся неравенство k ≤ n – k +1, то k изменяется от 0 до 
. Применяя правило суммы, приходим к соотношению F(n) = + + + …+ .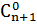
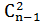Данное равенство можно доказать иначе: по свойству сочетаний 
= 
+ 
. Легко заметить, что последовательность чисел Фибоначчи обладает схожим свойством: F(n) = F(n – 1) + F(n – 2).
Процесс последовательных разбиений.
Заметим, что для решения комбинаторных задач часто применяют такой метод – устанавливают для задачи рекуррентное соотношение и показывают, что оно совпадает с рекуррентным соотношением для другой задачи, решение которой нам уже известно. Если при этом совпадают и начальные члены последовательностей в достаточном числе, то обе задачи имеют одинаковые решения.
Перечислим ещё свойства, которыми обладают числа последовательности Фибоначчи:
· Число Фибоначчи 
есть ближайшее целое число к 
, т. е. к n-му члену геометрической прогрессии (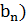
, первый член которой 
, а знаменатель равен а. (это свойство доказывается с помощью записи формулы Бине и установления того факта, что абсолютная величина разности между членом последовательности Фибоначчи и членом данной прогрессии меньше 
.
Если использовать теорию пределов, то легко
можно показать, несколько видоизменив доказательство этой
теоремы, что
= 0.
Пользуясь доказанной теоремой, можно вычислять
числа Фибоначчи при помощи таблиц логарифмов.
Вычислим например вычислим 
.
a = 
= 1,6180 
= 14∙ 
- 
= 2,5762
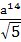= 376,9
Ближайшее целое число к 376, 9 является число 377, это и есть .
При вычислении чисел Фибоначчи с большими
номерами мы уже не сможем по таблицам
логарифмов определить все цифры числа, а сможем указать
только несколько первых цифр его, так что
вычисление окажется приближенным.
· Свойства чисел Фибоначчи, связанные с делимостью:
1. Соседние числа Фибоначчи взаимно просты.
2. Число Фибоначчи четно тогда и только тогда, когда его номер делится на 3.
3. Число Фибоначчи делится на 3 тогда и только тогда, когда его номер делится на 4.
4. Число Фибоначчи делится на 4 тогда и только тогда, когда его номер делится на 6.
5. Число Фибоначчи делится на 5 тогда и только тогда, когда его номер делится на 5.
6. Число Фибоначчи делится на 7 тогда и только тогда, когда его номер делится на 8.
7. Число Фибоначчи делится на 16 тогда и только тогда, когда его номер делится на 12.
(Эти свойства можно доказать, используя свойства делимости чисел, алгоритм Евклида, индукцию, а также свойство биномиальных коэффициентов: «если р – простое, а k≠0 и k≠p, то 
делится на р»).
· Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
· Производящей функцией последовательности чисел Фибоначчи является:
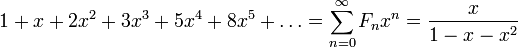
· Суммы биномиальных коэффициентов на диагоналях треугольника Паскаля являются числами Фибоначчи.
