Муниципальное общеобразовательное учреждение
МОУ лицей №29
РЕФЕРАТ
на тему:
Рекуррентно заданные числовые последовательности
Выполнил: Яковлев Дмитрий
ученик 10 класса
Учитель: Топчий
Елена
Александровна
Тамбов 2012
Содержание
| Введение | |
| 1. Последовательность Фибоначчи | 4 - 8 |
| 2. Свойства последовательности Фибоначчи | 9 - 12 |
| 3. Последовательность Фибоначчи и золотое сечение | |
| 4. Задачи, связанные с последовательностью Фибоначчи | 14 - 18 |
| 5. Числа Каталана | 19 -25 |
| Заключение | |
| Список литературы и других источников | |
ВВЕДЕНИЕ
Данная исследовательская работа посвящена рассмотрению некоторых числовых последовательностей, заданных рекуррентно, их свойств и задач с ними связанных. Этого материала нет в школьной программе, при изучении числовых последовательностей мы сталкиваемся с рекуррентным заданием лишь на примере арифметической и геометрической прогрессий, но изучение таких последовательностей – достаточно увлекательный процесс.
Теория по данному вопросу достаточно простая, лаконичная, пронизывающая все разделы математики, применимая как в геометрии, так и в математическом анализе. Задачи, рассмотренные в этой работе, принадлежат крупнейшим математикам. Основы этой теории были впервые опубликованы в середине восемнадцатого века. В последние годы изменился кругозор читателей математической литературы, и многие достижения в теории чисел, упоминаемые в популярной литературе, не подкреплены знаниями читателей. Поэтому хотелось бы рассмотреть одни из самых известных последовательностей, заданных рекуррентным способом, изучить их свойства и значимость в истории развития математики.
Последовательность Фибоначчи
Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума
их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Кроме Франсуа Виета, жившего, впрочем, уже в шестнадцатом столетии, и математиков более близких нам времен, школьный курс математики не называет ни одного имени, относящегося к средним векам. Это, конечно, не случайно. Математика в эту эпоху развивалась
чрезвычайно медленно, и крупных математиков тогда было очень мало.
Тем больший интерес представляет для нас сочинение «Liber abacci» («Книга об абаке»), написанная знаменитым итальянским математиком Леонардо из Пизы, который известен больше по своему прозвищу Фибоначчи (Fibonacci-—сокращенное filius Bonacci, т. е. сын Боначчи). Эта книга, написанная в 1202 г.,
дошла до нас во втором своем варианте, который относится к 1228 г.
«Liber abacci» представляет собой объемистый труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший заметную роль в развитии математики в Западной Европе в течение нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими («арабскими») цифрами. Сообщаемый в «Liber abacci» материал поясняется на большом числе задач, составляющих значительную часть этого трактата.
Среди многих задач он привёл следующую:
«Пара кроликов приносит раз в месяц приплод из двух крольчат (самца и самки), причём молодые крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?»
Из условия задачи следует, что через месяц будет две пары кроликов. Через месяц приплод даст только первая пара кроликов, и получится три пары. А ещё через месяц приплод дадут и исходная пара кроликов, и пара кроликов. Появившихся два месяца тому назад. Поэтому всего будет пять пар кроликов.
Перейдем теперь от кроликов к числам рассмотрим следующую числовую последовательность:
F(n): 1; 2; 3; 5; 8; 13; 21; 34; …
в которой каждый член равен сумме двух предыдущих членов, т. е. при всяком
n > 2
F(n) = F(n – 1) + F(n – 2) или an = an—1 + an – 2 (1)
Такие последовательности, в которых каждый член определяется как некоторая функция предыдущих (причём равенство (1) может содержать некоторые коэффициенты перед an—1 и an – 2), часто встречаются в математике и называются рекуррентными или, по-русски, возвратными последовательностями.
Понятие возвратной последовательности является широким обобщением понятия арифметической или геометрической прогрессии. Как частные случаи оно охватывает также последовательности квадратов или кубов натуральных чисел,
последовательности цифр десятичного разложения рационального числа (и вообще любые периодические последовательности), последовательности коэффициентов частного от деления двух многочленов, расположенных по возрастающим степеням х, и т. д. Отсюда видно, что с возвратными последовательностями в курсе математики средней школы приходится встречаться весьма часто. Теория возвратных последовательностей составляет особую главу математической дисциплины, называемой исчислением конечных разностей. Основы теории возвратных последовательностей были разработаны и опубликованы в двадцатых годах восемнадцатого века французским математиком Муавром и одним из первых по времени членов Петербургской Академии наук швейцарским математиком Даниилом Бернулли. Развёрнутую теорию дал крупнейший математик восемнадцатого века петербургский академик Леонард Эйлер, посвятивший возвратным последовательностям тринадцатую главу своего «Введения в анализ бесконечно-малых».
Количество слагаемых в правой части равенства (1) определяет порядок возвратной последовательности. Само равенство (1) называют уравнением возвратной последовательности.
Заметим, что по одному только рекуррентному условию нельзя вычислить члены последовательности, т. к. по такому условию можно составить бесконечно много последовательностей. Для однозначного построения последовательности необходимо задать дополнительные условия – несколько первых членов.
У последовательности Фибоначчи начальными членами являются две единицы.
До сих пор мы определяли число Фибоначчи рекуррентно, т. е. индуктивно, по их номеру. Оказывается число этой последовательности можно определить и непосредственно, аналитически – как некоторую функцию номера.
Исследуем для этого различные последовательности, удовлетворяющие соотношению (1).
Все такие последовательности будем называть решениями уравнения (1).
Будем обозначать буквами V, V/ и V// соответственно последовательности
v1, v2 , v3, …
v1/, v2/, v3/ , …
v1//, v2//, v3//, …
Есть две простые леммы:
1)Если V есть решение уравнения (1), и с - произвольное число, то последовательность cV есть также решение данного уравнения.
2) Если последовательности V и V" являются решениями уравнения (1), то и их сумма также является решением данного уравнения.
Пусть теперь V/ и V// два непропорциональных решения уравнения (1), т. е. такие, что при любом постоянном С найдётся такой номер n, что 
Покажем, что всякую последовательность V можно представить в виде:
C1V/ + C2V// (2), где C1 и C2 - некоторые постоянные.
Т. к. последовательности V/ и V// непропорциональны, то непропорциональны и её соответствующие члены (это утверждение можно доказать методом от противного, применив индукцию).
Теперь найдём последовательность V, она будет определена, если заданы её два начальных члена.
Чтобы V = C1V/ + C2V// , найдём такие с1 и с2, чтобы имела место система:
c1v1/ +c2v1// = v1,
c1v2/ + c2v2// = v2.
Тогда на основании двух лемм, указанных ранее, C1V/ + C2V// даст нам последовательность V.
В силу непропорциональности последовательностей, эта система будет разрешима относительно c1 и c2, каковы бы ни были при этом числа v1, v2. 

Знаменатель этих дробей не может быть равен нулю. а подставив полученные значения в C1V/ + C2V// мы и получим требуемое представление последовательности V.
Для получения всех решений уравнения V = C1V/ + C2V// , нам достаточно найти два его какие-нибудь непропорциональные решения.
Будем искать эти решения среди геометрических прогрессий. В соответствии с леммой №1, мы имеем право выбрать только такие прогрессии, первый член которых равен 1.
Итак. возьмём прогрессию: 1; q; q2; …
Чтобы она являлась решением уравнения V = C1V/ + C2V// , необходимо. чтобы для любого n выполнялось qn – 2 + qn – 1 = qn или 1 + q = q2 .
Корни этого квадратного уравнения  и
и 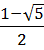 .
.
с1 + с2 = 1 и
с1  + с2
+ с2 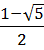 =1
=1
Решив эту систему, получим:
с1 =  , с2 =
, с2 =  ,
,
откуда V =  .
.
Эта формула называется формулой Бине (по имени получившего её математика).
Полученная формула и есть аналитическое задание последовательности Фибоначчи F(n).






