Бiрiншi шектiк есеп немесе Пуассон теңдеуi үшiн
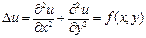 (2)
(2)
Дирихле есебi: Қандай да бiр G облысының iшiнде (2) теңдеудi қанағаттандыратын, ал Г шекарасында
 (3)
(3)
шартын қанағаттандыратын 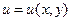 формуласын табу керек, мұндағы
формуласын табу керек, мұндағы 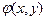 – берiлген үзiлiссiз функция.
– берiлген үзiлiссiз функция.
 және
және  қадамдарын сәйкес х және у деп таңдап, тор тұрғызамыз
қадамдарын сәйкес х және у деп таңдап, тор тұрғызамыз  және әрбiр iшкi
және әрбiр iшкi  түйiнiнде
түйiнiнде 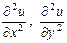 туындыларын (1) ақырлы айырымдар қатынасымен алмастырып (2) теңдеудi мына түрде жазамыз:
туындыларын (1) ақырлы айырымдар қатынасымен алмастырып (2) теңдеудi мына түрде жазамыз:
 (4)
(4)
мұндағы 

 функциясының мәндерiне қатысты сызықтық алгебралық теңдеулер жүйесiн бередi.
функциясының мәндерiне қатысты сызықтық алгебралық теңдеулер жүйесiн бередi.
Дербес жағдай. Егер G облысы тiк төртбұрыш және  болса, онда (4) теңдеулер былайша жазылады:
болса, онда (4) теңдеулер былайша жазылады:


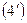
Егер  болғанда (2) Лаплас теңдеуі деп аталады.
болғанда (2) Лаплас теңдеуі деп аталады.
 және сәйкес ақырлы-айырымдық теңдеулер келесi түрде жазылады:
және сәйкес ақырлы-айырымдық теңдеулер келесi түрде жазылады:


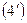 және
және  теңдеулердi жазған кезде келесi түйiндер сұлбасы қолданылды:
теңдеулердi жазған кезде келесi түйiндер сұлбасы қолданылды:

2-сурет
Дифференциалдық теңдеудi айырымдық теңдеумен алмастыру қателiгi, яғни Лаплас теңдеуi үшiн қалдық мүше  келесi теңсiздiкпен бағаланады:
келесi теңсiздiкпен бағаланады:

мұндағы

Айырымдық әдiспен алынған жуықтаң шешiмнiң қателiгi келесi үш қателiктерден құралады:
1. Дифференциалдық теңдеудi айырымдық теңдеумен ауыстырғандағы қателiктен;
2. Шеттiк шарттарды жуықтау қателiгiнен;
3. Айырымдық теңдеулер жүйесiн жуықтап шешу нәтижесiнде пайда болатын қателiктерден.
МЫСАЛ
Қабырғасы 1-ге тең, оқшауланған жазық шаршы пластинкадағы жылудың станционар үлестірімі туралы есепті пластинканың шекарасында температура тұрақты болған жағдайда қарастырайық.

3-сурет
Температураның үлестірімін беретін  (
( ,
,  ) функциясы Лаплас теңдеуінің шешімі болатыны белгілі:
) функциясы Лаплас теңдеуінің шешімі болатыны белгілі:
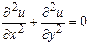
Берілген есеп үшін шекаралық шарттар 3-суретте көрсетілген.
Шешуі:
 қадаммен тор құрамыз, тоғыз ішкі тораптар аламыз. Осы тораптарда ақырлы-айырымдық теңдеулер құрамыз.
қадаммен тор құрамыз, тоғыз ішкі тораптар аламыз. Осы тораптарда ақырлы-айырымдық теңдеулер құрамыз.
Шекаралық шарттардың симметриялылығын
 11=
11=  31,
31,  12=
12=  32,
32,  13=
13=  33 (1)
33 (1)
Бұл  функциясының ішкі тораптардағы белгісіз мәндерінің санын тоғыздан алтыға дейін азайтады.
функциясының ішкі тораптардағы белгісіз мәндерінің санын тоғыздан алтыға дейін азайтады.
Осылайша (3,1), (3,2), (3,3) тораптарда ақырлы-айырымдық теңдеулерді жазудың қажеті жоқ. Қалған ішкі (1,1), (2,1), (1,2), (2,2), (1,3), (2,3) тораптарда сәйкес алты теңдеуді аламыз:


Бұл теңдеулер құрамына тағы функцияның шекаралық нүктедегі 12 мәні кіреді. Ол мәндерді біз шекаралық шарттардан аламыз:
 (3)
(3)
Қалған тораптарға шекаралық шарттар қолданылмайды.
(2), (3) шарттарды ескере отырып, нақты түрде келесі жүйені аламыз:

Бұл жүйені Гаусс әдісімен шешіп, алатынымыз:







