 функциясы берiлген және оның мәндерi
функциясы берiлген және оның мәндерi  кесте түрiнде берiлген.
кесте түрiнде берiлген. 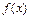 – функциясы сияқты
– функциясы сияқты  – кез келген функциясы да
– кез келген функциясы да  нүктелерiнде дәл сондай мәндердi қабылдайды, ал берiлген аралықтағы өзге нүктелерде
нүктелерiнде дәл сондай мәндердi қабылдайды, ал берiлген аралықтағы өзге нүктелерде  функциясының қабылдайтын мәнiне, таңдалынған дәлдiкпен алғандағы, маңайлас шамаға тең.
функциясының қабылдайтын мәнiне, таңдалынған дәлдiкпен алғандағы, маңайлас шамаға тең.
 функциясын берiлген тораптардан өзге нүктелерде
функциясын берiлген тораптардан өзге нүктелерде  функциясымен алмастырса, мұндай операцияны
функциясымен алмастырса, мұндай операцияны  функциясын интерполяциялау деймiз. Мұнда
функциясын интерполяциялау деймiз. Мұнда  формуласы интерполяциялау формуласы деп аталады. Интерполяциялау формулалары
формуласы интерполяциялау формуласы деп аталады. Интерполяциялау формулалары  функциясының аргументтiң берiлген мәндерi қарастырылған аралықта белгiсiз мәндерiн табу үшiн қолданылады.
функциясының аргументтiң берiлген мәндерi қарастырылған аралықта белгiсiз мәндерiн табу үшiн қолданылады.
Нәтижесiн шығарар кезде мынадай қателiктер ескерiледi:
1. Әдiс қателiгi
2. Жойып алмау қателiгi
3. Жуықтау қателiгi.
Әдiстiң қателiгi қалған мүшенi
интерполяциялау формуласы арқылы табылуы мүмкiн және 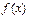 – тiң сәйкес дәрежесiндегi туындысының интерполяциялау аралығындағы мәнiне байланысты бағаланады.
– тiң сәйкес дәрежесiндегi туындысының интерполяциялау аралығындағы мәнiне байланысты бағаланады.
9.2. Тең емес арақашықтықта орналасқан түйiндерге арналған Лагранждың интерполяциялық формуласы
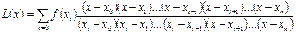 (1)
(1)
Айталық,  функциясы
функциясы  аралығында тек
аралығында тек  -ге дейiнгi барлық дәрежеде туындысы табылады және қателiгi мына түрде болады.
-ге дейiнгi барлық дәрежеде туындысы табылады және қателiгi мына түрде болады.
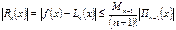 (2)
(2)
 ,
,

9.3. Тең емес арақашықтықта орналасқан түйiндерге арналған Ньютонның интерполяциялық формуласы
 (3)
(3)
(3)-тiң оң жағындағы барлық мүшелерiнiң қосындысы Ньютонның интерполяциялау көпмүшелiгi деп, ал соңғы мүшесi
 (4)
(4)
қателiгi деп аталады.
9.4. Эйткеннің интерполяциялау сұлбасы
 Функциясын есептегенде
Функциясын есептегенде  -тiң нақты мәндерiн тең емес арақашықтықта орналасқан аргументтерi үшiн Лагранждың интерполяциялау полиномы арқылы Эйткеннiң сұлбасын қолдану тиiмдi.
-тiң нақты мәндерiн тең емес арақашықтықта орналасқан аргументтерi үшiн Лагранждың интерполяциялау полиномы арқылы Эйткеннiң сұлбасын қолдану тиiмдi.

 (5)
(5)
…………………………………….


болсын және Эйткен сұлбасы бойынша есептеу төмендегi сұлба түрiнде жүргiзiледi:

| 
| 
| 
| 
| 
| |

| 
| 
| ||||

| 
| 
| 
| |||

| 
| 
| 
| 
| ||
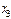
| 
| 
| 
| 
| 
| |
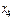
| 
| 
| 
| 
| 
| 
|
Есептеу соңғы 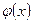 -тiң тiзбектiк мәнiн салыстырумен анықталады.
-тiң тiзбектiк мәнiн салыстырумен анықталады.
9.5. Ньютонның бірінші интерполяциялау формуласы
Тұрақты қадаммен берілген кесте, функцияға ақырлы түрлі кестесі құрылған. Интерполяциалау көп мүшелігін осындай түрде іздейміз:
 (6)
(6)
Бұл n дәрежедегі көпмүшелік.
 коэфиценттерінің мағынасын, шыққан функцияның мағынасының сәйкестік шартын және көпмүшелік түйіндерін табамыз.
коэфиценттерінің мағынасын, шыққан функцияның мағынасының сәйкестік шартын және көпмүшелік түйіндерін табамыз. 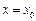 -ге қарап, (5.11)-ден
-ге қарап, (5.11)-ден  -ді табамыз, одан
-ді табамыз, одан  .
.  мәнді
мәнді  және
және  -ні бере отырып төмендегіні аламыз:
-ні бере отырып төмендегіні аламыз:
 , одан
, одан 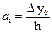

тағы сол сияқты  , немесе
, немесе 
одан 
 .
.
Жалпы жағдайда 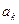 үшін мынадай түр болады:
үшін мынадай түр болады:
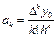 (7)
(7)
(6)-ші көпмүшелік үшін (7)-ні қоямыз:
 (8)
(8)
Бұл формула басқаша түрде қолданылады
 болса, тағы сол сияқты
болса, тағы сол сияқты 
онда: 

 (9)
(9)
(9) – формула Ньютонның бірінші интерполяциондық формуласы деп аталады. Абсолюттік шамасы бойынша  кіші болғанда, бұл формула интерполяцианың кесіндісінің басында интерполяциалау үшін қолданылады. Осы себепке байланысты Ньютонның бірінші интерполяциалау формуласын алға интерполяциалау деп атайды. Бастапқы
кіші болғанда, бұл формула интерполяцианың кесіндісінің басында интерполяциалау үшін қолданылады. Осы себепке байланысты Ньютонның бірінші интерполяциалау формуласын алға интерполяциалау деп атайды. Бастапқы  мәнін
мәнін  аргументтегі кестелік мәнді қабылдауға болады.
аргументтегі кестелік мәнді қабылдауға болады.
9.6. Ньютонның екінші интерполяциялау формуласы
Аргументтің мәні интерполяциалау кесіндісінің соңына жақын орналасқан кезде бірінші интерполяциалау формуласын қолдану тиімсіз. Бұл жағдайда артқа интерполяциалау, яғни, Ньютонның келесі түрде ізделінетін екінші интерполяциалау формуласы қолданылады:
 (10)
(10)
Ньютонның бірінші формуласындағыдай  коэффицентері түйінде функция мәндері және интерполяциалау көпмүшесінің сәйкес келу шартынан табылады.
коэффицентері түйінде функция мәндері және интерполяциалау көпмүшесінің сәйкес келу шартынан табылады.
 (11)
(11)
(11)-шы өрнекті (10)-ші өрнекке қойып және  айнымалысына өтіп, Ньютонның екінші формулаларының соңғы түрін аламыз:
айнымалысына өтіп, Ньютонның екінші формулаларының соңғы түрін аламыз:
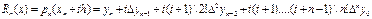 (12)
(12)
9.7. Интерполяциалау көпмүшелігінің қателігі
Егер  интерполяциалау функциясы аналитикалық түрде белгілі болса, онда интерполяциалау қателігін (әдіс қателігі) бағалауға арналған формуланы қолдануға болады.
интерполяциалау функциясы аналитикалық түрде белгілі болса, онда интерполяциалау қателігін (әдіс қателігі) бағалауға арналған формуланы қолдануға болады.  интерполяциалау көпмүшелігінің қалдық мүшесі мынадай болады:
интерполяциалау көпмүшелігінің қалдық мүшесі мынадай болады:

Бекітілген кесіндісі үшін интерполяциалау көпмүшелігінің бір ғана екендігінен, қателігі туралы сұрақты баяндау Лагранж көпмүшелігі мен Ньютон көпмүшелігіне бірдей.
 функциясының
функциясының  -ге дейінгі барлық туындыларды бар болсын деп ұйғарайық, R-тұрақты көбейткіш деп қосымша функция енгіземіз:
-ге дейінгі барлық туындыларды бар болсын деп ұйғарайық, R-тұрақты көбейткіш деп қосымша функция енгіземіз:
 (13)
(13)
Байқап отырғанымыздай,  функциясының (
функциясының ( ) түбірлері (
) түбірлері ( -интерполяциалау тораптары) бар. R-коэффициентін
-интерполяциалау тораптары) бар. R-коэффициентін  әрбір
әрбір  нүктесінде (
нүктесінде ( )-ші түбір болатындай етіп таңдап аламыз. Шынында
)-ші түбір болатындай етіп таңдап аламыз. Шынында  , яғни
, яғни
 болуы үшін
болуы үшін
 (14)
(14)
болуы жеткілікті. Сонымен,  функциясының R мағынасы интерполяциалаудың кесіндісінде
функциясының R мағынасы интерполяциалаудың кесіндісінде  түбірін иемденді және
түбірін иемденді және  кесінділерінің әрқайсысының соңында 0-ге айналды:
кесінділерінің әрқайсысының соңында 0-ге айналды:
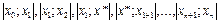
Кесінділердің әрқасыларына Рош теоремасын қолдана отырып, мынаған көз жеткіземіз:
 кем дегенде
кем дегенде 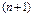 түбіріне ие.
түбіріне ие.
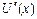 кем дегенде
кем дегенде 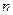 түбіріне ие.
түбіріне ие.
 кем дегенде бір түбірді иемденеді.
кем дегенде бір түбірді иемденеді.
 -ні
-ні  болатын нүктенің өзі деп белгілейік (13),
болатын нүктенің өзі деп белгілейік (13),  -рет дифференциялаймыз.
-рет дифференциялаймыз.

бұдан 

 кезінде
кезінде
 (15)
(15)
(14) пен (15)-ті салыстырсақ

Бірақ  нүктесі туынды (шынында
нүктесі туынды (шынында  -қа бағынышты!). Сондықтан былай жазуға болады.
-қа бағынышты!). Сондықтан былай жазуға болады.

Егер  -ті қабылдасақ, онда
-ті қабылдасақ, онда
 (16)
(16)
Бағалау формуласын (5.21) Лагранж формуласы бойынша интерполяциялаудың әдіс қателігін есептеуге тікелей қолданса болады.  және
және  алмастыруды қолдана отырып (16) формуласынан Ньютон формулалары бойынша интерполяциалаудың қателіктерін бағалау формуласын алуға болады.
алмастыруды қолдана отырып (16) формуласынан Ньютон формулалары бойынша интерполяциалаудың қателіктерін бағалау формуласын алуға болады.
 (17)
(17)
 (18)
(18)
Лагранж және Ньютонның интерполяцияланған көпмүшелерінің талдауы, сондайақ (16), (18) бағалау формулаларының талдаулары. Пайдалы практикалық қортындыларын жасауға мүмкіндік береді.
Қателік мән мағынасына  шамасы шешімді әсер етеді, ол түйінді нүктелерді интервалының ортасынан
шамасы шешімді әсер етеді, ол түйінді нүктелерді интервалының ортасынан  алынған жағдайда азайтылады. Сонымен қатар,
алынған жағдайда азайтылады. Сонымен қатар,  екі түйінді мағыналардың ортасына жақын болғанда
екі түйінді мағыналардың ортасына жақын болғанда  түйіндерінің жұп сандарын алған тиімді (
түйіндерінің жұп сандарын алған тиімді ( түйіндерінен сол жақтан және
түйіндерінен сол жақтан және  -тен оң жақтан)
-тен оң жақтан)
Егер  түйінді мағыналардың біріне жақын болса,
түйінді мағыналардың біріне жақын болса,  түйіндердің тақ санын пайдалануға болады.
түйіндердің тақ санын пайдалануға болады.
Ньютонның интерполяцияланған формулаларын тәжірибеде құрастыру кезінде сәйкес соңғы қалдықтары нөлге тең немесе жақын мүшелерді елемеу керек. Сондықтан, тәжірибелік есептеулерде Ньютонның интерполяцияланған формулалары берілген дәлдік шегінде тұрақты деп саналатын қалдықтарға ие мүшелерге бөлінеді.
Соңғы қалдықтармен Ньютон формулалары бойынша интерполяциалау дәлдігі арасындағы байланыс келесі түсініктемелермен бекітіледі.
Назар аударамыз:  аз мәнінде және
аз мәнінде және  үздіксіз жағдайда, шамамен есептеуге болады:
үздіксіз жағдайда, шамамен есептеуге болады:
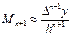
мұнда 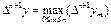
яғни, 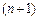 ретіндегі соңғы қалдықтар модульдерінен максималды. Сонымен (17) және (18).
ретіндегі соңғы қалдықтар модульдерінен максималды. Сонымен (17) және (18).
Ньютонның бірінші және екінші интерполяциялау формулаларының қалдық мүшелерін бағалау жағдайлары мынадай түрге ие:
 (19)
(19)
 (20)
(20)
(19) және (20) формулалары  туынды интерполяциялаушы
туынды интерполяциялаушы  функциясын зерттемей ақ интерполяциалау әдісінің қателігін бағалауға мүмкіншілік беретіндігімен ыңғайлы (соның ішінде,
функциясын зерттемей ақ интерполяциалау әдісінің қателігін бағалауға мүмкіншілік беретіндігімен ыңғайлы (соның ішінде,  аналитикалық формуласы тіптен белгісіз болғанда).
аналитикалық формуласы тіптен белгісіз болғанда).
Интерполяциалау соңғы қателігіне есептеу қателігі де әсер етеді. Бұл мәселелерді толық зерттеу аз қиындықтар тудырмайды мысалы сенімді және көп мәнді есептеу кестелерін құрастыру кезінде.
Разрядтардың үлкен санымен және кестелердің автоматтандырылған басылымдарымен есеп жүргізуге мүмкіндік беретін ЭЕМ-гі қолданумен техникалық жұмыс бірталай жеңілдейді.
9.8. Функция кестесін тығыздау
Функцияның кестесін тығыздау үшін интерполяциалау қолданылады. Функцияның берілген кестесі бойынша аргументтің мәнін үлкейту арқылы жаңа кестені құру операциясы кейбір жағдайда функцияны субтабуляциялау деп аталады. Егер кесте тұрақты қадаммен берілген болса, онда Ньютонның интерполяциалау көпмүшелігін қолданған жөн. ЭЕМ-де есептеу үшін түйіндік нүктелері белгілі болған жағдайда (егер ақырлы айырымдар және полином дәрежесі қолмен есептелінген болса) Ньютон формулаларын Горнер кестесі арқылы көрсетуге ыңғайлы болады. Ньютонның бірінші интерполяциалау формуласы келесі түрде көрсетіледі:

Егер Горнер кестесін қолдансақ  мәнін циклда есептеуімізге болады. Егер қолданылатын ақырлы айырмдардың максималды реті үлкен болмаса, онда
мәнін циклда есептеуімізге болады. Егер қолданылатын ақырлы айырмдардың максималды реті үлкен болмаса, онда  мәнін Ньютон формулалары арқылы табуға болады.
мәнін Ньютон формулалары арқылы табуға болады.
МЫСАЛ 1.
Мына мәндер кестесi үшiн Лагранж көпмүшелiгiн құрып  -тi есептеңiз:
-тi есептеңiз:
| x | ||||
| y |
Шешуi. төмендегi жағдайда n=3, онда 

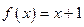 сызықтық функциясы интерполяциялациялау көпмүшелiгi болып табылады, онда
сызықтық функциясы интерполяциялациялау көпмүшелiгi болып табылады, онда
Жауабы: 
 .
.
МЫСАЛ 2.
 функциясының мәндер кестесi берiлген.
функциясының мәндер кестесi берiлген.
| x | ||||||
| y | 3.0000000 | 3.0043214 | 3.00806002 | 3.0128372 | 3.0170333 | 3.0211893 |
n=3 жоғарғы Ньютонның бiрiншi формуласын қолданып, lg1001 есептеп және R3 -қалдық мүшесiн бағалап көрсетiңiз.
Шешуi.

 үшiн,
үшiн, 
| x | y | 
| 
| 
|
| 3.0000000 | 0.0043214 | -0.0000426 | 0.0000008 | |
| 3.0043214 | 0.0042788 | -0.0000418 | 0.0000009 | |
| 3.00806002 | 0.0042370 | -0.0000409 | 0.0000008 | |
| 3.0128372 | 0.0041961 | -0.0000401 | ||
| 3.0170333 | 0.0041560 | |||
| 3.0211893 |
 -тi есептеймiз:
-тi есептеймiз:

 -тi есептеймiз:
-тi есептеймiз:

 -тi есептеймiз:
-тi есептеймiз:

Осыдан,

қалдық мүшенi бағалаймыз
 ,
,
мұндағы  Егер
Егер  , онда
, онда  , сондықтан
, сондықтан 
 және
және  болса
болса

болады.
Жауабы: 
Бақылау сұрақтары:
1. Кестемен берілген функцияны интерполяциалау әдісімен жуықтаудың ерекшелігі неде?
2. Интерполяциалау көпмүшелігінің табылуы мен жалғыздығы қалай негізделеді? Оның дәрежесі интерполяциалау түйіндерімен қалай байланысады?
3. Лагранж және Ньютонның интерполяциалау көпмүшеліктері қалай құрылады? Бұл интерполяциалаудың екі әдісінің ерекшкліктері қандай?
Дәріс. Сандық интегралдау. Интегралдық тегістеу. Интерполяциялық квадратуралық формулалары. Ең жақсы алгебралық дәлдікті квадратуралық формулалар.






