13.1. Торлар әдісі
Торлар әдiсi немесе ақырлы айырымдар әдiсi қазiргi кезде дербес туындылы теңдеудi шешудiң кеңiнен тараған сандық әдiстерiнiң бiрi. Бұл әдiс бойынша туынды ақырлы-айырымдық қатынаспен алмастырылады.
Оxу жазықтығында Г шекарасы бар қандай бiр G облысы берiлсiн.
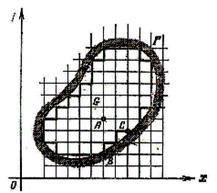
1-сурет
Жазықтықта екi параллель түзулер үйiрiн тұрғызайық
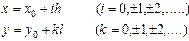
Осы түзулердiң қиылысу нүктесi түйiн деп аталады. Егер екi түйiн Ох немесе Оу осiнiң бағытымен бiр-бiрiнен сәйкес 
немесе 
тор қадамына тең қашықтықта болса, онда олар көршi түйiндер деп аталады. Барлық төрт көршi түйiндер осы D облысына тиiстi болса, онда түйiндер iшкi түйiндер деп аталады.
Егер көршi төрт түйiннiң ең болмағанда бiреуi D облысына тиiстi емес болса, онда түйiндер шекаралық түйiндер
арқылы 
iзделiндi
функцияның тор түйiндерiндегi мәндерiн белгiлейiк.
Әрбiр iшкi 
түйiнде дербес туындыны айырымдық қатынаспен алмастырайық:
Шеттiк нүктелерде келесi формулаларды қолданамыз:
Осылайша, екiншi реттi дербес туындылар алмастырылады
(1)
Көрсетiлген алмастырулар тордың әрбiр түйiндерiнде дербес туындылы теңдеулердi шешу – айырымдық теңдеулер жүйесiн шешуге келiп тiреледi.
