Коши есебін қарастырайық. 
арқылы ізделінді шешімнін 
нүктесіндегі жуык мәнін белгілейік. Рунге-Кутт әдісі бойынша ізделінді функцяның мәндер тізбегін есептеу формуласы
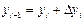
мұндағы
Бағалау қателігі
мұндағы 
– 
нүктесіндегі берілген теңдеудін шешімінін дәл мәні,
- мәндері h/2 және h қадаммен алынған жуық мәндер.
МЫСАЛ 1.
Коши есебінің [0; 0,2] кесіндіде e=10-5 дәлдігімен жуық шешімін табу керек
Шешуі. Бастапқы жуықтауды келесі түрде аламыз
осыдан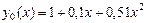 
. (3)-ші формуланы қолдансақ
(4)
.
Келесі айырым x =0,2 болғанда e мәнінен үлкен болады
(4) өрнектегі соңғы екі қосындылардын косындысы e шамасынан кіші, сондықтан 
келесі түрде алуға болады
Келесі айырым [0; 0,2] кесіндісінде e мәнінен кіші
Жауабы: 
МЫСАЛ 2.
Коши есебімен
анықталған, қадамы 
болғанда у функциясының төрт мәнін Эйлер әдісін қолдана отырып табу керек.
Шешуі. Бастапқы шарттан 
сондықтан аргумент мәндері
у функциясының мәндері
Жауабы:
| х | 0,1 | 0,2 | 0,3 | 0,4 | |
| У | 1,1 | 1,22 | 1,36 | 1,52 |
МЫСАЛ 3.
Бірінші ретті дифференциалдық теңдеудің шешімін Рунге-Кутт әдісімен табу керек
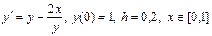
Шешуі.
Есептің шарты бойынша 
Осыдан
болғанда
.
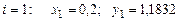Осы сияқты 
мәндеріне сәйкес 
функция мәндерін табамыз.
13,14,15-Дәрістер. Математикалық физика есептерін шешудің сандық әдістері. Дербес туындылы теңдеудiң сандық шешiмi Пуассон теңдеуіне қойылған айырымдылық Дирихле есебінің жинақтылығы мен орнықтылығы.
13.1. Торлар әдісі
