(2)-ші келтірілген сызықтық теңдеулер жүйесі берілсін. Түбірдің бастапқы жуықтауын еркін түрде таңдаймыз. Зейдель әдісі бойынша түбірдің 
+1 жуықтауын келесі формула бойынша есептейміз
Итерация әдісінде қарастырылған шарттар Зейдель әдісі үшін де тура. Зейдель әдісі итерация әдісіне қарағанда жақсы жинақталады.
МЫСАЛ 1.
Сызықтық алгебралық теңдеулер жүйесін итерация әдісімен 
болғанда шешу керек
Шешуі. Берілген жүйені (2) түрге келтіру үшін 
және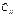 
коэффициенттерін табамыз
(4) шарттарды табылған С іj қанағаттандырады
,
,
.
Осыдан (3) жүйені аламыз:
Бастапқы жуықтау ретінде бос мүшелерді аламыз
.
Бірінші жуықтау 
Екінші жуықтау 
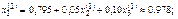
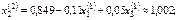
(6) теңсіздікті тексереміз
, 
, 
.
(6) шарттар орындалмаған соң келесі үшінші жуықтауды есептейміз, яғни к=3 болғанда
үшінші және екінші жуықтаударда табылған 
-тердің мәндері (6) теңсіздікті қанағаттандырады
, 
, 
.
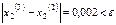Сондықтан, итерация процесін тоқтатып, жауабын аламыз
МЫСАЛ 2.
Сызықтық алгебралық теңдеулер жүйесін Зейдель әдісімен 
болғанда шешу керек
.
Шешуі. Итерация процесіндегі келтірілген жүйені келесі түрде аламыз
Бастапқы жуықтау ретінде итерация әдісімен табылған мәндерді аламыз: 
.
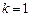
Жауабы: 
.
Бақылау сұрақтары:
1. Бастапқы жуықтауды таңдаудың итерациялық әдістердің итерациялық процестерінің сызықтық алгебралық теңдеулер жүйесінің шешіміне жинақталуына әсері қандай?
2. Зейдель әдісінің итерациялық процесінің қарапайым итерацияның итерациялық процесінен қандай өзгешілігі бар?
