Гаусс әдісі белгісіздерді біртіндеп жою негізінде әртүрлі сұлба бойынша іске асырылуы мүмкін. Есептеу сұлбасын қандай да бір нақты мысалда қарастырған ыңғайлы. Сондықтан төртінші ретті теңдеулер жүйесін қарастырайық:
(1)
(
– бас элемент деп аталады) деп ұйғарайық. Гаусс әдісімен (1) сызықтық алгебралық теңдеулер жүйесін шешу процесі үшбұрышты теңдеулер жүйесін
(2)
құрумен пара-пар. Бас элементтің нөлден өзге болуы Гаусс әдісінің қолданылуының қажетті және жеткілікті шарты болып табылады.
Гаусс әдісінің тура жүрісі -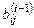 
коэффициенттерін табу
1) 
,
2) 
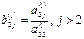, мұнда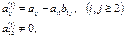 
3) 
, мұнда 
4) 
.
Гаусс әдісінің кері жүрісі – белгісіздердің мәнін есептеу процесі.
МЫСАЛ.
Сызықтық алгебралық теңдеулер жүйесін Гаусс әдісімен шешу керек
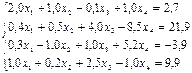(3)
Шешуі.Тура жүрісі
1) 
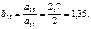
яғни (2) жүйенің бірінші теңдеуін аламыз:
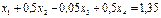
2) 
яғни (2) жүйенің екінші теңдеуін аламыз
яғни (2) жүйенің үшінші теңдеуін аламыз:
.
Сонымен, берілген (3) жүйеге пара-пар жүйе жазамыз:
(4)
