Жартылай Қақ бөлу (дихотомия) әдісі

(1) теңдеу берілсін. функциясы кесіндісінде үзіліссіз болсын және (2) теңсіздік орындалсын. кесіндіде жатқан (1) теңдеудің түбірін табу үшін осы кесіндіні қақ ортасынан бөлеміз.

Егер болса, онда берілген теңдеудің түбірі болып табылады, ал кері жағдайда, егер ,

онда кесіндіні қарастырамыз, әйтпесе кесіндіні қарастырамыз.

Әрі қарай 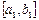, яғни 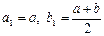немесе кесіндісін тағы қақ бөлеміз. Нәтижесінде қандай да бір қадамда не (1) теңдеудің дәл түбірін аламыз, не бір бірінің ішінде орналасқан 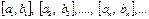шектеусіз тізбектерді аламыз.

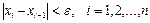(3)

жағдайда итерациялық процесті тоқтатамыз. Шешімнің қателік бағасының формуласы

.

 

МЫСАЛ 1.

 

теңдеудің түбірлері жатқан аралықты табу керек.

Шешуі.

1) , яғни ;

2) Осы функциялардың графиктерін саламыз

 

 

3) .

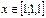4) ,

яғни .

Жауабы: .

МЫСАЛ 2.

теңдеудің [1; 1,1] кесіндісінде жататын түбірін жартылай (қақ) бөлу әдісімен дәлдігі e=0,01 болғанда табу керек.

Шешуі.

1қадам. 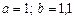, онда

, ,

яғни (2) теңсіздік орындалмайды, сондықтан келесі кескінін қарастырамыз .

2 қадам. , онда ;

, ,

яғни (2) теңсіздік орындалмайды. (3) теңсіздікті тексереміз

 

.

Сондықтан 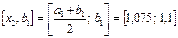кескінін қарастырамыз.

3 қадам. онда ;

 

,

(3) теңсіздікті тексереміз:

 

,

 

сондықтан кескінін қарастырамыз.

4 қ адам. , онда ;

, ,

 

яғни (2) теңсіздік орындалады. (3) теңсіздікті тексереміз

.

Жауабы: .

 

Бақылау сұрақтары:

1. Теңдеулерді шешуде сандық әдістерді қолданудағы түбірді бөлу этапы немен аяқталады?
2. Графикалық тәсілмен түбірді бөлу есептеулер арқылы қалай іске асырылады? Бұл жағдайда бір айнымалыдан тәуелді функциялардың қай қасиеттері қолданылады?