теңдеуінің x түбірі 
кесіндісінде жекеленген, үзіліссіз және анықталған таңбаны сақтайтын, сонымен қатар 
кесіндісінде үзіліссіз болсын. Ньютон әдісі у= f (x) қисығынын доғасын қисыктың қандайда бір нүктесінде жүргізілген жанамамен алмастырғанмен пара-пар.
Жанамалар (Ньютон) әдісінің негізгі формуласы:
(6)
Қателік бағасы
мұндағы х* - түбірдің дәл мәні;
x - түбірдің жуық мәні.
МЫСАЛ 1.
теңдеудің [1; 1,7] кесіндісінде жататын түбірін хорда әдісімен дәлдігі e=0,01 болғанда табу керек.
Шешуі. 
, ал 
, яғни бірінші жағдай болады, сондықтан (4) формуланы қолданамыз.
1 -қадам. [1; 1,7] қарастырамыз:
, 
.
2 -қадам. [1,588; 1,7] қарастырамыз:
, 
.
3 -қадам. [1,639; 1,7] қарастырамыз:
, 
.
4-қ адам. [1,642; 1,7] қарастырамыз:
, 
.
Жауабы: 
МЫСАЛ 2.
теңдеуінің [1; 1,7] кесіндісінде жататын түбірін жанамалар (Ньютон) әдісімен дәлдігі e=0,01 болғанда табу керек.
Шешуі. 
, 
, 
.
Мұнда 
және 
, сондықтан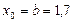 
.
1 -қадам. 
2- қадам. 
3 -қадам. 
Жауабы: 
, егер e=0,01.
Бақылау сұрақтары:
1. x=f(x) теңдеуін жамалара әдісі арқылы шешуде берілген ε дәлдікті алудың критериі қандай шарттар болады?
2. Хорда және Ньютон әдістерінің геометриялық түсініктемелері қандай?
