10. Кез келген матрицаны қандай да бір санға көбейтуге брлады, яғни егер 
саны және
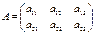
матрицасы берілген болса, онда олардың көбейтіндісі деп
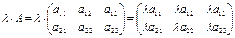
матрицасын айтады.
Бұл жерде матрицаны санға көбейту дегенімізден оның барлық элементін осы санға көбейту керек екендігін көреміз. Керісінше, егер матрицаның барлық элементтерінің ортақ көбейткіші болса, оны матрица белгісінің сыртына көбейткіш ретінде шығаруға болдады.
Ал анықтауышта осындай ортақ көбейткішті әрбір жатық жолдан немесе әрбір тік бағанадан жеке-жеке анықтауыш белгісінің алдына сыртына шығаруға болады. Керісінше, анықтауыштыбір санына көбейту үшін оның тек бір жатық жолын немесе тек бір тік бағанасын осы санға көбейту жеткілікті.
20. Тек мөлшерлері бірде матрицаларды ғана қосуға болады, мысалы,
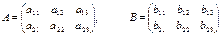
матрицаларының қосындысы деп мына
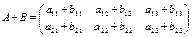
матрицаны айтады, яғни қосынды матрицаның элементтері қосылғыш матрицалардың сәйкес элементтерін қосу арқылы табылатынын көреміз.
30. Матрицаларды өзара көбейту. Екі матрицаны өзара көбейту ерекше ереже бойынша іске асырылады, яғни өзімізге үйреншікті екі санды көбейту ережесінен өзгеше екендігін ескереміз. Жалпы алғанда кез келген екі матрицаны көбейтуге болмайды. Оларды көбейту үшін ол көбейткіш матрицалардың мөлшерлері ерекше үйлесулері керек: бірінші көбейткіш матрицаның тік бағаналар саны екінші көбейткіш матрицаның жатық жолдар санына тең болуы шарт. Жалпы 
матрицасының мөлшері 
болса, онда оны 
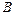матрицасына көбейту үшін 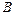матрицасының мөлшері 
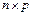болуы шарт.
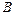Сонымен осы екі және матрицаларын көбейтіп мөлшері 
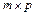болатын үшінші бір С матрицасын аламыз және оның кез келген элементі 
мына формула
бойынша табылатын болады.
Ескерту. Кез келген квадрат матрицаны сол реттегі бірлік 
матрицасына екі жағынан да (оң және сол) көбейтуге болатынын және осы көбейтулердің нәтижесінде бастапқы матрицасының өзі шығатынын, яғни
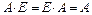
ескерейік.
Анықтама. Квадрат матрицасының анықтауышы нөлге тең болса, онда ондай матрицаны ерекше матрица деп, ал керісінше, оның анықтауышы нөлден айрықша болса, онда ерекше емес матрица деп атайды.
