Математикалық есептерде кездесетін қателіктерді негізінен бес топқа бөледі:
1) Есеп қателіктері, басқаша айтқанда, математикалық есептің берілуімен байланысты қателіктер. Қандайда бір құбылыстың математикалық сипаттамасы нағыз құбылыспен үнемі дәл келе бермейді: әдетте олар тек қана салыстырмалы түрде қандайда болмасын идеал модель бейнесінде беріледі. Табиғаттың қандайда бір құбылысын зерттеу барысында біз есепті жеңілдету мақсатында белгілі бір шарттарды қабылдауға мәжбүр боламыз бұл әрекер бірқатар қателіктердің тууына себеп болады.
Әдіс қателігі. Кей жағдайда есепті тура қойылымында шешу қиын немесе тіпті мүмкін емес. Бұл жағдайда берілген есепті нәтижесі жуықталған түрде берілген есеп нәтижесіне тең болатын басқа есеппен ауыстыруға тура келеді. Осы кезде әрине қателік пайда болады, мұндай қателік түрін әдіс қателігі деп атайды. Мысалы, аналитикалық түрде берілген есепті сандық есеппен алмастыру әдіс қателігіне жатады.
2) Қалдық қателіктері, басқаша айтқанда, математикалық анализдегі шексіз процесстермен байланысты қателіктер. Математикалық формулаларда қолданылатын функциялар шексіз тізбектер немесе қатарлар түрінде берілуі сирек емес. (мысалы, 
). Тіптен көптеген математикалық теңдеу-лерді – шектері (lim) осы теңдеулердің шешімдері болып табылатын шексіз процестерді сипаттау арқылы ғана шешуге болады. Шексіз процесс, жалпы айтқанда, белгілі бір қадамнан кейін (шектеулі қадамда) бітпейтіндіктен, біз осы тізбектің қандайда бір мүшесінде теңдеудің жуықталған шешімін алдық деп тұжырымдап тоқтауға мәжбүр боламыз. Процесті бұлай тоқтату әрине қателікті тудырмай қой-майды.
3) Дөңгелектеу қателіктері. Санау жүйелерімен байланысты қателіктер. Тіптен ондық санау жүйелерінде рационал сандарды өрнектеу барысында, үтірден кейін оң жақта орналасатын цифрлар саны шексіз болуы мүмкін. Мысалы, 
рационал сан, ондық бөлшек түріне келтіргенде 
периодты санына тең болады. 
десек, нәтижесінде 
қателігін аламыз. Иррационал сандарды да осы түрде дөңгелектеуге тура келеді.
4) Әрекет қателіктері. Жуықталған сандарға қолданылатын әрекеттермен байланысты қателіктерді айтады. Жуықталған сандарға қандайда бір әрекеттер қолдана отырып, біз нәтижені де жуықтап табамыз. Бұл жағдайда әрекет қателіктері түзетілмейтін қателіктер болып табылады.
5) Бастапқы қателіктер. Математикалық формулаларда мәні тек қана жуықтап анықталатын сандық параметрлердің болуымен байланысты қателіктер. Мысалы, барлық физикалық тұрақтылар осындай сандық параметрлер қатарына жатады.
Бақылау сұрақтары:
- Есептеу эксперименті дегеніміз не?
- Есептерді сандық әдістерді қолданып шешуде қандай талаптар орындалуы керек?
- ЭЕМ-де есептерді шешу барысында қателіктердің қандай түрлері болуы мүмкін?
- Айталық х -кейбір шаманың дәл мәні, ал а жуық мәні болатын болсын. Сонда
жуықтауының абсолюттік қателігі дегеніміз не? - Қандай да
-шамасының а -жуықтауының салыстырмалы қателігі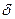 
-саны дегеніміз не?
