ІІІ. ДӘРІСТІК САБАҚ КОНСПЕКТІЛЕРІ
Дәріс. Сандық әдістер» пәніне кіріспе. Қателіктер теориясы.
Пәнге кіріспе.
Ателіктер теориясы.
Ателіктердің классификациясы.
Пәнге кіріспе.
Жаңа технологияның өркендеуі және инженерлік зерттеулерге математикалық әдістердің кеңінен қолданылуы, сол сияқты есептеу техникаларының көптеп шығарылуы, олардың сапасының жоғарылауы халық шаруашылығының көптеген саласында электрондық есептеу машиналарын кеңінен қолданылуға әкелді. Қазір ғылыми-техникалық есептердің көбінің ойдағыдай шешілуі көп жағдайда электрондық есептеу машиналарын жедел қолдана білуден тәуелді. Осы мақсатқа жету үшін күшті және ыңғайлы, үлкен және шағын әмбебап, дербес компьютерлер ғана емес, жақсы өңделген сәйкес сандық әдістер арсеналы да қажет.
«Сандық әдістер» пәні орта буын программистерді даярлауға қажетті негізгі курстардың бірі болып табылады. Пәннің алдына қойған мақсаты:
- студенттерде қолданбалы есептерді шешудің сандық әдістері туралы, математикалық модельдеу мен есептеу эксперименті туралы түсінікті қалыптастыру;
- әртүрлі ғылыми-техникалық есептерді шешуде ЭЕМ-н қолданудың жалпы түсінігін тереңдету мен жетілдіру.
- студентті сандық әдістердің кейбір құралдарымен қаруландыру;
- студентті таңдаған әдісін негіздеуге, нақтылықты бағалаудың жолдарын көруге, қолданатын әдістің алгоритмін құра білуге, сәйкес программаны құра білуге машықтандыру;
- курсқа сәйкес программалық жабдық даярлап, студентке оны қолдану әдісін үйрету.
«Сандық әдістер» курсы екі тараудан тұрады: «Жуықтап есептеулер», «Математикалық талдаудың сандық әдістері». Бірінші тарау келесі бөлімдерді қамтиды: «Қателіктер теориясы»; «Бір айнымалы сызықты емес теңдеулерді шешу»; «Сызықты алгебралық теңдеулер жүйелерін шешу»; «Сызықтық программалау»; «Функциялардың жуықтауы. Интерполяциалау және экстраполяциалау». Екінші тарау келесі бөлімдерді қамтиды: «Сандық дифференцалдау»; «Сандық интегралдау»; «Дифференциалдық теңдеулерді шешу»; «Экперименталдық мәліметтерді өңдеу»; «Математикалық физика есептерін сандық әдістермен шешу».
«Сандық әдістер» пәнін меңгеру әр тақырып бойынша көптеген есептерді шығармай мүмкін емес. Сондықтан әр бөлімнің соңында оларды шешу өтілген материалды меңгеруге мүмкіндік туғызатын көптеген жаттығулар келтіріледі.
Ателіктер теориясы
ателіктерді қатаң ескеріп есептеулер
Белгілеулерді енгіземіз: х- кейбір шаманың нақты мәні, а - х санының жуық мәні.
Анықтама 1. Шаманың нақты және жуық мәндерінің айырмасының модулі жуықтаудың абсолютті қателігі деп аталады және ∆ арқылы белгіленеді, яғни
(1)
Анықтама 2. Жуықтаудың шекті абсолютті қателігі деп ∆а>0 саны аталады,
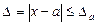(2)
Анықтама 3. Жуықтаудың салыстырмалы қателігі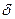 
келесі қатынаспен анықталады:
(3)
Анықтама 4. Жуықтаудың шекті салыстырмалы қателігі деп δа>0, δ≤ δа санын атаймыз. Келесі формула орын алады:
(4)
