4.1. Загальні відомості. Розв’язання складних геометричних задач супроводжується великою кількістю графічних побудов, що ускладнює аналіз та розуміння креслення. Для отримання розв’язку задачі з мінімальною кількістю побудов використовують методи перетворення ортогонального креслення. Всі методи, які використовуються в нарисній геометрії ділять на дві групи:
- методи, в яких об’єкт проекціювання залишається незмінним, а система П1, П2, П3 доповнюється новими площинами проекцій П4, П5, П6;
- положення площин проекцій П1, П2, П3 залишається незмінним, а змінюється положення об’єкта проеціювання.
Такі перетворення дозволяють значно скоротити кількість побудов на кресленні.
4.2. Метод заміни площин проекцій. Суть методу полягає в тому, що в систему з площин проекцій П1, П2, П3 послідовно вводять нові площини П4, П5, П6, які дозволяють отримати нове положення геометричного образу та спростити розв’яза-ння задач.
В процесі перетворення зберігається ортогональний метод проекціювання. Тобто вісі проекцій розташовані завжди перпендикулярно до ліній проекційного зв’язку.
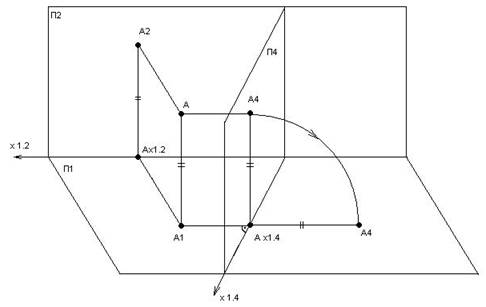
Розглянемо суть методу на об’ємній моделі Монжа (рис. 4.1).
В цьому випадку в системі площин проекцій Рис. 4.1
П1/П2 замість площини П2 вводять нову площину П4 і отримують нову систему П2/П4. Точку А проекцюють на П4 (А4), на вісі Х1.4 отримують проекцію Ах1.4. Потім суміщають П4 з П1 та відмічають рівні відрізки AzAx1.2=AA1=Ax1.4A4.
Приклад. Побудувати проекції точки А на П4 та П5.
1. Площини П1/П2 заміняють на П1/П4. Х1.4 ^ А1А4, А2Ах1.2=Ах1.4А4.
2. Площини П1/П2 заміняють на П2/П5.
Х2.5 ^А2А5, А1Ах1.2=Ах2.5А5 (рис. 4.2). Рис. 4.2
4.3. Розв’язання метричних та позиційних задач. Розв’язання метричних і позиційних задач розглянемо на конкретних прикладах.
Приклад 1. Визначити натуральну величину відрізка АВ заміною П1/П2 на П1/П4.
Для того, щоб визначити натуральну величину АВ треба перевести його із загального положення до прямої рівня, у якої одна з проекцій паралельна до вісі Х.
Х 1.4 ║А1В1.
Приклад 2. Відрізок АВ перевести із загального в проекцююче положення.
Рис. 4.3 Розв’язання цієї задачі складається з двох етапів:
1) пряму із загального положення переводять в пряму рівня (рис 4.3);
2) пряму рівня переводять до проекцюючої прямої Х 4.5┴А4В4.
Приклад 3. Визначити відстань між мимобіжними прямими АВ та СD.
Для розв’язання цієї задачі необхідно:
1) одну з мимобіжних прямих перевести із загального положення до проекцюючого;
2) 
з цієї точки опустити перпендикуляр на проекцію іншої прямої;
3) побудувати проекції перпендикуляра на всіх площинах проекцій.
1. П1/П2→П1/П4 x 1.4║C1D1.
2. x 4.5┴C4D4.
3. C5K5┴A5B5=K5;
(C5K5 – відстань).
4. K4 є A4B4.
5. K4L4┴C4D4.
6. K1 є A1B1;
L1 є C1D1.
7. K2 є A2B2;
L2 є C2D2 (рис. 4.4). Рис. 4.4
Приклад 4. Визначити натуральну величину ∆АВС.
В цьому випадку необхідно:
1) виконати дві заміни площин проекцій;
2) в результаті першої заміни перевести (АВС) із загального положення до проекцюючого;
3) в результаті другої заміни нову площину проекцій розташувати паралельно до площини трикутника, на якій і отримати розв’язок.
План розв’язання.
1. П1/П2→П1/П4.
Для виконання перетворень необхідно виконати умову Рис. 4.5
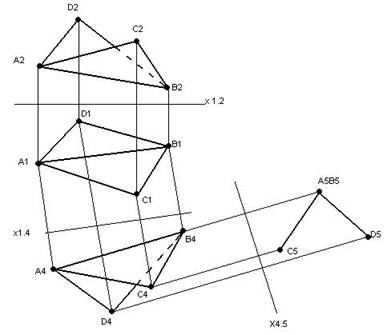перпендикулярності двох площин (трикутника та П4), а тому в площині трикутника будуємо горизонталь:
h є ABC;
x 1.4┴h.
2. П1/П4→П4/П5;
х 4.5 ║А4В4С4 (рис. 4.5).
Контроль правильності рішень: ∆АВС – найбільший на кресленні.
Приклад 5. Визначити величину двогранного кута.
Для розв’язання цієї задачі необхідно двогранний кут перетворити Рис. 4.6
в лінійний, при цьому ребро двогранного кута АВ перевести із загального положення в проекцююче.
1. П1/П2→П1/П4;
Х 1.4║А1В1.
2. П1/П4→П4/П5
Х 4.5┴ А4В4;
<C5A5B5 (рис. 4.6).
