6.1. Перетин граних поверхонь площиною. Результатом перетину граної поверхні з площиною є замкнута ламана лінія. Для побудови точок цієї лінії використовують допоміжні січні площини або інші методи в залежності від конкретних умов задачі. Головним елементом рішення задач є визначення точок, які одночасно належать до січної площини та геометричної поверхні.
Приклад 1. Побудувати лінію перетину призми площиною Г.
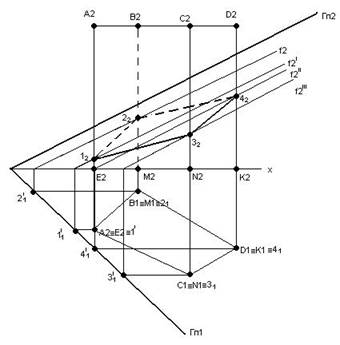Г – площина загального положення.
Призма розташована на П1.
Її бічні грані – горизонтально-проекцюючі площини, а ребра – горизонтально-проекцюючі прямі, які мають на П1 збиральні властивості, а тому горизонтальна проекція лінії перетину співпадає з проекцією
Рис. 6.1 призми на П1.
1. A1≡11; B1≡21; C1≡31; D1≡41.
Подальше розв’язання задачі зводиться до побудови фронтальних проекцій точок 1, 2, 3, 4, які одночасно належать призмі і площині Г. Для цього використовуємо фронталі площини Г.
2. f2/×A2E2=12.
3. f2×B2M2=22.
4. f2///×C2N2=32.
5. f2//×D2K2=42.
На П2 з’єднуємо 12, 22, 32, 42 відрізками прямих, враховуючи те, що 22 є невидима.
1232,3242 – видимі.
1222, 2242 – невидимі (рис. 6.1).
Приклад 2. Побудувати лінію перетину піраміди з площиною ∑ та визначити натуральну величину перерізу (рис. 6.2).
Аналіз графічної умови:
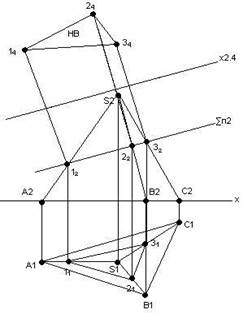- ∑ - фронтально-проекцююча площина, а тому ∑п2 має збиральну властивість;
- у зв’язку з цим позначаємо точки перетину ∑п2 з боковими ребрами піраміди;
- натуральну величину визначаємо методом заміни площин проекцій.
1. ∑п2×S2A2=12;
∑п2×S2B2=22;
∑п2×S2C2=32.
2. 11 є S1A1;
21 є S1B1;
31 є S1C1.
3. П1→П4;
х2.4║122232;
Рис. 6.2 ∆142434 – НВ.
6.2. Перетин поверхонь обертання площиною. В результаті перетину поверхонь обертання площиною утворюється замкнута крива лінія. Загальна послідовність розв’язання задач полягає у наступному:
1) використовуємо допоміжні січні площини окремого положення;
2) будуємо лінію перетину заданої поверхні з допоміжною січною площиною;
3) будуємо лінію перетину допоміжної і заданої площин;
4) позначаємо точки перетину лінії перетину поверхні з допоміжною площиною з лінією перетину площин.
Приклад: Побудувати лінію перетину конусу з площиною ∑ (рис. 6.3).
План розв’язання.
1. Будуємо проекції крайньої верхньої та нижньої точок перетину, використовуючи допоміжну горизонтально-проекцюючу площину Г.
1. Г┴П1.
2. Г1┴∑п1;
Г1 є S1.
3. Г1×K1=1121.
4. Г×∑=3,4.
5. 3242×S222=A2;
3242× S212=B2.
6. A1B1 є Гп1.
2. Будуємо проекції крайньої правої та лівої точок лінії перетину. Для цього використовуєо допоміжну січну площину ∆║П2.
7. ∆║П2;
∆П1║х;
∆П1 є S1.
8. ∆×∑= f;
f2×S252=C2;
f2×S262=D2;
C1D1 є ∆П1.
9. Θ║ П1;
Θ×K= R.
10. Θ×∑=h;
h1×R1=E1, F1;
E2, F2 є Θ2.
Рис. 6.3
На П1 лінія перетину – видима замкнута крива.
На П2 лінія перетину має дві частини: видиму і невидиму.
Межові точки видимості – крайня права і ліва точки (С2, D2)
А2, Е2 – видимі
С2, D2, B2, F2 – невидимі.
6.3. Перетин прямої та поверхні. В результаті перетину прямої та поверхні утворюються дві точки: входу та виходу.
Для побудови їх проекцій необхідно:
1) пряму заключити у допоміжну січну площину окремого положення;
2) побудувати лінію перетину поверхні з допоміжною площиною;
3) позначити точки перетину заданої прямої з лінією перетину поверхні площиною;
4) визначити видимість прямої, яка на інтервалі точок входу-виходу невидима.
Приклад 1. Побудувати точки перетину прямої l та піраміди (рис. 6.4).
1. l є Г;
Г┴П2.
2. 122232 є Г2.
3. 11 є S1A1;
21 є S1B1;
31 є S1C1.
4. l1×1131=K1;
l1×2131=L1;
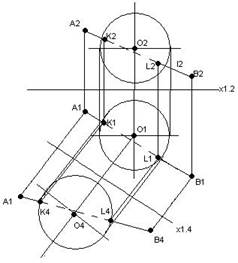K2, L2 є Г2. Рис. 6.4
Деякі задачі розв’язують за допомогою методу заміни площин проекцій.
Приклад 2. Побудувати точки перетину прямої l та сфери (рис. 6.5).
1. П1/П2→П1/П4;
х1.4║А1В1;
K4L4.
2. K1L1; K2L2.
Рис. 6.5
