При побудові площини в просторі будемо використовувати аналогії для прямої лінії на площині. Як і для прямої лінії можемо стверджувати, що між множиною всіх площин простору і множиною лінійних рівнянь відносно трьох змінних 
існує взаємно однозначна відповідність.
Нехай в просторі задана точка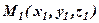 
і ненульовий вектор 
. Через точку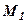 
можна провести єдину
Рис.11
площину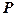 
перпендикулярно вектору 
. Щоб отримати рівняння
площини, виберемо на ній довільну точку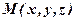 
і розглянемо
вектор 
(див. рис. 11).
Точка 
тоді і тільки тоді, коли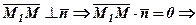 
— рівняння площини що проходить через дану точку з нормальним вектором.
Розкривши дужки в (17) маємо
— загальне рівняння площини, де позначено 
.
Отже, площині 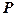відповідає лінійне рівняння (18). Навпаки, якщо задано лінійне рівняння вигляду (18), то неважко знайти точку 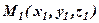, координати якої задовольняють це рівняння, і записати вектор . Вектор 
і точка визначають єдину площину .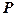
