а) Рівняння прямої за двома точками  і
і  знаходимо з канонічного рівняння (7) оскільки напрямний вектор
знаходимо з канонічного рівняння (7) оскільки напрямний вектор  , то
, то

Приклад. Записати рівняння прямої, якщо  ,
,  . Відповідь:
. Відповідь:  .
.
б) Відстань від точки  до прямої
до прямої  знаходиться за формулою
знаходиться за формулою

Дійсно, з рис. 8 зрозуміло, що
 ,
,

Рис. 8.
де  – довільна точка прямої. Вектор
– довільна точка прямої. Вектор  .
.
Тоді  Але із загального рівняння прямої
Але із загального рівняння прямої  , тому
, тому  а
а  . Отже,
. Отже,
отримуємо (9).
Наприклад, відстань від точки  до прямої
до прямої  за формулою (9) дорівнює
за формулою (9) дорівнює

в) Кут між двома прямими  і
і  спочатку знайдемо, коли їх рівняння мають вигляд (див. рис.9)
спочатку знайдемо, коли їх рівняння мають вигляд (див. рис.9)


Рис.9
Оскільки  а
а  , то
, то

Отже, 
– формула тангенса кута між двома прямими.
Зауваження. З рис.9 видно, що між прямими  і
і  - два кути: один – гострий
- два кути: один – гострий  , другий – тупий
, другий – тупий  . Згідно формули (11)
. Згідно формули (11)  - це той кут між прямими
- це той кут між прямими  і
і  , на який потрібно повернути пряму
, на який потрібно повернути пряму  проти годинникової стрілки від носно їх точки перетину до суміщення її з прямою
проти годинникової стрілки від носно їх точки перетину до суміщення її з прямою  . У формулі (11) для однозначності нагадує стрілка
. У формулі (11) для однозначності нагадує стрілка 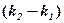 , записана зверху.
, записана зверху.
Приклад. В рівнобедреному прямокутному трикутнику АВС відома вершина прямого кута С(-1,2) і рівняння гіпотенузи АВ  . Скласти рівняння катетів.
. Скласти рівняння катетів.
Розв’язання. Рівняння прямої, що проходить через точку С знаходимо за формулою пучка прямих  , де кутовий коефіцієнт
, де кутовий коефіцієнт 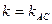 для прямої АС і
для прямої АС і  для прямої ВС.
для прямої ВС.
За умовою ÐА=ÐВ=45°, tg45°=1, тому  і
і  знаходимо за формулою (11), ураховуючи зауваження до неї.
знаходимо за формулою (11), ураховуючи зауваження до неї.

Спочатку знайдемо  і рівняння катета АС.
і рівняння катета АС.
Оскільки поворот прямої АВ на кут 45° проти годинникової стрілки відносно точки А приводить до суміщення з прямою АС, то у формулі (11)  , а
, а  . Із рівняння АВ:
. Із рівняння АВ:  , тому
, тому 

За формулою пучка рівняння прямої АС запишеться

(АС)  .
.
Аналогічно знайдемо  і рівняння ВС. При вершині В за формулою (11) відповідно беремо
і рівняння ВС. При вершині В за формулою (11) відповідно беремо  , а
, а  , ÐВ=45°
, ÐВ=45°
 Рівняння прямої ВС:
Рівняння прямої ВС:

(ВС) 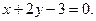
Якщо  – прямі паралельні, то
– прямі паралельні, то 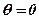 і тоді
і тоді

– умова паралельності двох прямих.
Якщо ж  , то
, то  , а
, а
 або
або

- умова перпендикулярності двох прямих.
Якщо ж прямі задані загальними рівняннями

то кут між ними можна знаходити, як кут між їх нормальними екторами  (див. рис. 10);
(див. рис. 10); 

Рис.10

косинус кута між двома прямими  і
і  , заданими загальними рівняннями.
, заданими загальними рівняннями.
Якщо  , то
, то

– умова паралельності. Якщо ж  , то
, то
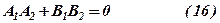
– умова перпендикулярності прямих.
г) Рівняння прямої, що проходить через задану точку  паралельно прямій
паралельно прямій  .
.
Розв’язання. Кожного разу, коли задається точка, то рівняння прямої краще знаходити за формулою (5) пучка прямих
 ,
,
де  – знаходимо із загального рівняння заданої прямої і умови паралельності прямих (12).
– знаходимо із загального рівняння заданої прямої і умови паралельності прямих (12).
Наприклад, скласти рівняння прямої, що проходить через точку 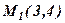 паралельно прямій
паралельно прямій  .
.
Розв’язання. Із загального рівняння прямої  , а за умовою паралельності прямих
, а за умовою паралельності прямих  , тоді отримуємо
, тоді отримуємо  .
.
д) Рівняння прямої, що проходить через точку  перпендикулярно прямій
перпендикулярно прямій  .
.
Із загального рівняння 
 , а за умовою перпендикулярності маємо
, а за умовою перпендикулярності маємо  , тоді шукане рівняння за формулою пучка
, тоді шукане рівняння за формулою пучка

Приклад. Скласти рівняння прямої, що проходить через точку 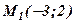 перпендикулярно до прямої
перпендикулярно до прямої  .
.
Розв’язання. Із 
 . Тоді
. Тоді
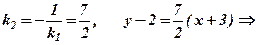
Відповідь:
 .
.
е) Точка перетину прямих  і
і  , якщо вони не паралельні
, якщо вони не паралельні
 знаходиться як розв’язок системи
знаходиться як розв’язок системи

Приклад. Знайти точку перетину прямих. Зробити рисунок, побудувавши графіки.

Розв’язання. Розв’яжемо дану систему рівнянь, домноживши перше рівняння на 2 і додавши результат з другим рівнянням


Підставивши  в перше рівняння маємо:
в перше рівняння маємо:

Отже, точка перетину  .
.
Побудуємо графіки за рівняннями, що входять в систему. Побудову краще виконати у відрізках на осях








