Z=f(x,y), M0(x0,y0), M(x,y)
Max ф-ции Z называется такое ее значение f(x0,y0),
которое является наибольшим среди всех
значений, принимаемых в некоторой окрестности
точки M0
Min ф-ции Z называется такое ее значение f(x0,y0),
которое является наименьшим среди всех
значений, принимаемых в некоторой окрестности
точки M0
Экстремум сущ. в тех точках, в которых частная
производная ф-ции Z=0 или не существует:
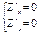
Если Z=f(x1,x2,...xn), то ¶Z/¶xi=0,
i=1,2,...n - необходимое условие.
Достаточный признак:

где A= Z``XX(x0,y0), C= Z``yy(x0,y0), B= Z``yx (x0,y0),
1) если D>0, то М0 - точка экстремума;
если А<0 или С<0, то М0 - точка max;
если А>0 или С>0, то М0 - точка min.
2) если D<0, то экстремума нет
3) если D=0, то вопрос о существовании
экстремума остается открытым.
Обратная матрица A-1, которая находится по формуле:

|
при этом A٠A-1=A-1٠A=E.
Правило (алгоритм) нахождения обратной матрицы
 .
.
- Вычислим det(A) A - невырожденная.
- Подсчитаем алгебраические дополнения Aij
 .
.
- Транспонируем матрицу A

- Составляем обратную матрицу по следующему правилу:
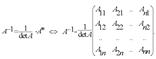
|
- Т Кронекера-Копелы Док-во:
Пусть система совместна ранг расширенной матрицы равен
рангу системы.
1)показать что дополнительный вектор столбец является
линейной комбинацией (т.к. из совместной системы следует
что Х1=С1б Хn=Cn при замене иксов на С получим что
система уравнений является линейной комбинацией доп.
столбца bjn т.к). системы это значит, что он не влияет на
ранг по свойству ранга и это значит, что ранг расширенной
матрицы равен рангу системы
2)ранги равны покажем что есть решение Пусть ранг
расширенной матрицы равен рангу системы Выделим базис
столбцы матрицы расширенной они же будут базис
столбцами матрицы системы. Предположим что базисными
являются первые r столбцов Согласно теореме о базисном
миноре (всякий столбец матрицы есть линейная комбинация
ее базисных столбцов) последний столбец может быть
линейной комбинацией базисных столбцов, т.е. существуют
числа С1,С1,Сr что С1аj1+C2aj2+,…,Crair=bir (2) если
подставить в уравнение системы
aj1X1,…,ajnXn=bjn (1) положим что
Х1=С1, Хr=Cr, Xr+1=0получим что все уравнения
системы (1) превратятся в (2) Т.е. получим
Х=(С1С2Сr0000)”вектор столбец”- решение
системы значит система разрешима.
Ранг не может быть больше числа столбцов: если
ранг расширенной матрицы равен числу столбцов то
у системы одно решение, если ранг меньше числа
столбцов то у системы множество решений.
-Док-во: Т о базисном миноре
Обозначим аik элементы матрицы
(k 1,…m строк, j=1,…n столбцов)
пусть С1С2Сn столбцы матрицы
пусть базисный минор находится
в столбце (Cj1, Cj2,…Cjr) и в
строках с номерами k1,…kr.
Доказать что для любого столбца
существует числа L1,…,Lr такие
что столбец является линейной
комбинацией столбцов
Cj=L1Cj1+,…+LrCjr (1)
Для элементов матрицы А с учетом
свойств матрицы уравнение (1) имеет
вид (1<k<m) aij=L1aij1+,…,Lrakir
где Lj не зависят от K.
-Док-во: Т Крамера
Если определитель отличен от нуля,
это достаточно для того, чтобы
матрица имела обратную А в минус
первой степени
АХ=В; Х=В/А; Х=В*А-1степени,
подставим в первое ур-е получим
А*В*Ав –1степени=В А*А в минус
первой степени единичная матрица,
следовательно, ЕВ=В; В=В
Допустим, что матрица А имеет
множество решений (
Х1, Х2, Хn) то АХ2=Ви АХ1=В
следовательно АХ2=АХ1
Умножим обе части на обратную
матрицу А получим ЕХ2=ЕХ1
следовательно, Х1=Х2 т.е. запись
(Х1Х2Хn) не имеет смысла и все иксы
равны. Формула Крамера ход: записать
Х=А в минус первой *В где В вектор
столбец свободных членов А в минус
первой обратная к А запишем обратная
матрица равна еденици деленой на
определитель матрицы А умноженное
на союзную матрицу,…
Базисным минором называется минор
отличный от нуля r-го порядка где r
ранг матрицы.
-Док-во обратной матр:
-По определителю обратной матрицы
А в минус первой степени = В;
АВ=ВА=Е следует
-А и А в минус первой степени
перестановочные квадратные
матрицы оного порядка по теореме
о произведении обратных матриц
имеем, что detA*detA в минус
первой степени=det(A*A в минус
первой степени)=detE=1=detA*detA
в минус первой степени из этого
следует, что ни один определитель
не может быть нулевым, если
матрица имеет обратную матрицу






