Расчет валов из условий прочности и жесткости

Расчет валов заключается в определении размеров поперечного сечения вала (диаметра сплошного вала или внешнего и внутреннего диаметров пустотелого вала) из условий прочности и жесткости.

Максимальное касательное напряжение в поперечном сечении вала определяется по формуле (12.11) и оно не должно превышать расчетного сопротивления срезу 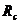, тогда условие прочности вала при кручении будет иметь вид:

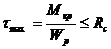                                                                                               (12.17)

где 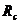  есть расчетное сопротивление материала при кручении, которое принимается равным 0,5 – 0,6 расчетного сопротивления при растяжении.

Условие прочности (12.17) содержит три величины: крутящий момент 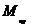, полярный момент сопротивления поперечного сечения вала  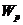и расчетное сопротивление 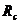. В зависимости от того, какие из этих величин известны, можно осуществлять:

1) Проверочный расчет. Он выполняется в случае, когда отсутствует проектная документация, но известны все три величиныи 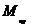, , 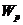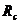. Чтобы быть уверенным в несущей возможности вала, проверяют выполнение условия (12.17). Если это условие выполняется, то вал может использоваться по назначению. Если условие не выполняется, то нужно уменьшить крутящий момент или увеличить диаметр вала.

2) Проектный расчет. Он заключается в определении размеров поперечного сечения вала из условия прочности (12.17).

Для сплошного поперечного сечения полярный момент сопротивления определяется формулой (12.12), то есть 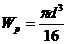, тогда из условия (12.17) найдем необходимый диаметр сечения:

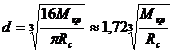                                                                                (12.18)

Для пустотелого поперечного сечения при отношении 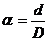, имеем

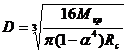                                       и 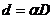                                             (12.19)

 

       3) Определение допустимой нагрузки на вал. Если известны размеры поперечного сечения вала и расчетное сопротивление 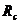, то из условия прочности легко найти максимальный крутящий момент, допустимый для вала:

                                                                                                                  (12.20)

       Аналогичные задачи можно решать при использовании условия жесткости. Чтобы составить это условие найдем относительный угол закручивания на участке длиной : 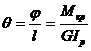. Эта величина не должна превышать допускаемых значений 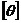. В результате получим условие жесткости вала:

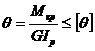                                                                                                               (12.21)

       При этом величины допускаемых углов закручивания 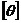 зависят от условий работы вала и предлагаются для использования в границах:

- при обычных условиях работы 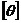= 0,0053 радиан/м.

- при переменных нагрузках 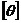= 0,0044 радиан /м.

- при внезапных нагрузках 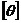= 0,0026 радиан /м.

Если проектный расчет вала выполняется с использованием условий прочности и жесткости, то диаметры вала принимаются по тому расчету, по которому имеют большие из значения.

 

Расчет винтовых цилиндрических пружин

С малым шагом

 

       В технике очень часто применяются винтовые цилиндрические пружины в качестве амортизаторов или аккумуляторов энергии. Например, рессоры вагонов, грузовых автомобилей, клапаны двигателей изготовляют с применением цилиндрических пружин. Они изготовляются из высокопрочной проволоки круглого поперечного сечения диаметра d и имеют витки среднего диаметра D с небольшим шагом (рис.12.5,а). Количество витков зависит от назначения пружины и принимается конструктивно, или рассчитывается. Вдоль оси цилиндрической пружины действуют внешние силы F растяжения или сжатия.

       Разрежем пружину на две части и рассмотрим равновесие верхней из них. Вдоль оси этой части пружины будут действовать внешняя сила F та продольная сила N=F (рис.12.5,б). Приведем эту силу к центру поперечного сечения проволоки путем замены ее действия поперечной силой Q=F и крутящим моментом М_кр = F· D/2 (рис.12.5,в).

 

                            

                                 

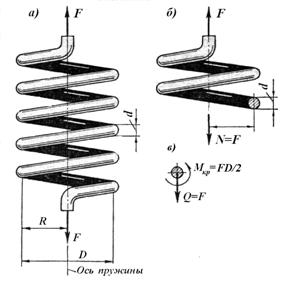
                                                           Рис.12.5

 

       От действия поперечной силы в плоскости сечения проволоки возникают касательные напряжения сдвига, которые приближенно можно считать равномерно распределенными по площади сечения. На рис.12.6,а начерчена эпюра касательных напряжений вдоль горизонтального диаметра проволоки. Эти напряжения будут определяться по формуле:

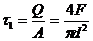                                                                                                               (12.22)

       От действия крутящего момента в плоскости сечения провода возникают касательные напряжения кручения, которые линейно зависят от положения точки сечения. На рис.12.6,б приведена эпюра касательных напряжений вдоль того же диаметра проволоки. Из этой эпюры видно, что максимальные напряжения возникают на внешних волокнах проволоки и определяются по формуле (11.11) предыдущего параграфа:

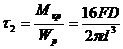                                                                                                        (12.23)

     Наибольшее суммарное напряжение возникает в той точке сечения, в котором направления напряжени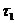й  и 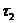 совпадают.                                                                                      

 

                          

 

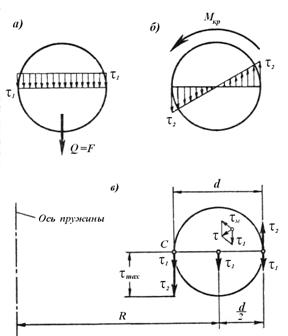
                                                        Рис.6.6

 

Как видно из рисунков 12.6,а и 12.6,б, такой точкой является точка С (левая точка сечения). Наибольшее напряжение в этой точке будет равняться:

                                                                                   (12.24)

       В случае, когда средний радиус витка пружины намного превышает диаметр проволоки, можно пренебречь вторым слагаемым, заключенным в скобках формулы (12.22). Тогда максимальные напряжения будут определяться зависимостью:

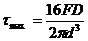                                                                                                                 (12.25)

       То есть, в этом случае расчет винтовой пружины выполняется только на кручение, а действие поперечной силы не учитывается.

       Пружины изготовляют из высококачественной стали. Поэтому расчетное сопротивление могут иметь значения: (200 – 800) МПа. Диаметр проволоки пружины определяется из условия прочности:

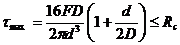                                                                                       (12.26)

        Кроме расчета на прочность, часто приходится определять деформацию пружины, то есть удлинение или укорочение начальной длины пружины (оседание пружины).

       Оседание пружины определяется по следующей формуле, которую приводим без доказательства:

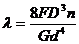                                                                                                                  (12.27)

где n – количество витков пружины.