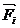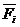По характеру связей твердого тела, загруженного пространственной системой сил, основные задачи статики можно разделить на несколько групп:
1. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных шарнирами, как с телом, так и с опорами.
2. Задачи о равновесии тела, имеющего ось вращения, которая закреплена с помощью цилиндрических подшипников. Подшипниками называют опорные устройства, позволяющие телу свободно вращаться вокруг оси, но препятствующие его свободному смещению в двух или в трех взаимно перпендикулярных направлениях. В последнем случае подшипник называют упорным или подпятником.
3. Задачи о равновесии тела, закрепленного при помощи сферического шарнира и дополнительных шарнирно стержневых связей.
4. Задачи о равновесии тела, опирающегося при помощи цилиндрических катков на плоскость или на специальные направляющие.
Решение задач любой группы следует начинать с анализа связей тела, с установления их характера и направлений сил, с которыми эти связи действуют на рассматриваемое тело. После этого необходимо выбрать рациональные направления координатных осей, записать условия равновесия и составить на их основе уравнения, решение которых позволяет найти величины и истинные направления реакций связей рассматриваемого тела.
Пример 6.1. Однородная плита весом G = 300 кН загружена горизонтальной силой F = 500 кН и удерживается в равновесии при помощи шести стержней, шарнирно соединенных с плитой в точках А, В, C, D и закрепленных шарнирно в неподвижных точках A1, B1, D1. Требуется определить реакции опорных стержней. Необходимые размеры указаны на рис.6.8.
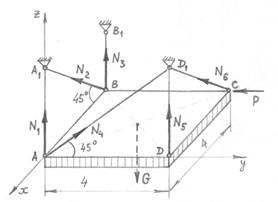
Рис.6.8
Решение. Известно, что реакция шарнирно закрепленного с двух сторон стержня направлена вдоль его оси. Используя это свойство, устанавливаем направления неизвестных реакций 
, 
, 
, 
, 
, 
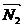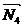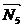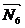, действующих на плиту (рис.6.8).
Выбираем прямоугольную систему координат с началом в точке А и её оси направляем так, чтобы наибольшее число сил было расположено в координатных плоскостях.
Так как плита находится в равновесии под действием заданных сил и реакций связей, то должны выполняться шесть условий равновесия:
, 
, 
, 
, 
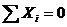Найдем проекции каждой силы на координатные оси и её моменты относительно тех же осей. Рассмотрим, к примеру, силу Её проекции на оси х. и y равны нулю, так как линия действия этой силы перпендикулярна к указанным осям. Проекция силы на ось z равна её модулю и имеет положительный знак, так как сила и ось z имеют одинаковые направления. Моменты рассматриваемой силы относительно всех координатных осей равны нулю, так как сила приложена в начале координат.
Рассуждая аналогично, устанавливаем проекции каждой силы на координатные оси, а также их моменты относительно тех же осей.
Для удобства и большей наглядности решения задачи все вычисления сведем в таблицу 6.1.
Таблица 6.1
| Силы | Проекции сил на оси координат | ||
| 
| 
| |
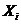
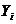
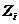
| 1 | 2 | 3 | 4 |
|
| 0 | 0 | N1 |
|
| 
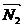
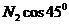
| 0 |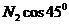
|
|
| 0 | 0 | N3 |
|
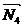
| 0 |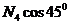 
|
|
|
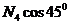
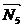
| 0 | 0 | N5 |
|
| 
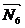
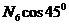
| 0 | -∙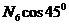
|
| 0 | -F | 0 |
| 0 | 0 | -G |
| Силы | Моменты сил относительно координатных осей | ||
| 
| 
| |
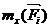
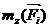
| 1 | 5 | 6 | 7 |
|
| 0 | 0 | 0 |
|
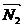
| 0 | 4∙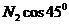
| 0 |
|
| 0 | 4∙N3 | 0 |
|
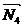
| 0 | 0 | 0 |
|
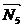
| 4∙N5 | 0 | 0 |
|
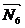
| 4∙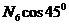
| 4∙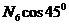
| -4∙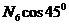
|
|
| 0 | 0 | 4F |
|
| -2∙G | -2∙G | 0 |
Суммируя по вертикалям выражения столбцов 2,3...7 этой таблицы, получаем следующие шесть уравнений с шестью неизвестными:
1) 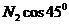+ 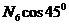= 0;
2) 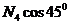- F = 0;
3) N 1 + 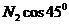+ N 3 + 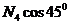+ N 5 + 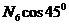-G = 0;
4) 4 N 5 + 4 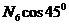- 2G = 0;
5) 4 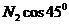+ 4 N 3 + 4 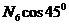-2G = 0;
6) 4 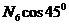- 4 F = 0.
После подстановки в эти уравнения значений заданных сил F = 500 кН
и G = 300 кН и решения их в приведенной ниже последовательности, находим:
- из уравнения 2)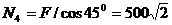 
кН.
- из уравнения 6)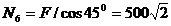 
кН.
- из уравнения 1)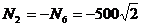 
кН.
- из уравнения 4) N5 = G/2- 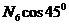=150-500=-350 кН.
- из уравнения 5) N3 = G/2- 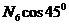- 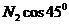=150 кН.
- из уравнения 3) N1 = 0.
Направления реакций , , 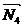, 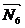имеющих положительные знаки, на рис.6.8 показаны правильно, а направления реакци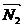й и 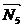, имеющих отрицательные знаки, в действительности противоположны направлениям, показанным на том же рисунке. При изменении направлений сил N2 и N5 следует одновременно исключить их отрицательные знаки их модулей, т.е. принять: N2 = 500 
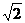кН. и N5 = 350 кН.
Пример 6.2. Подъемный поворотный кран установлен на трехколесной тележке ABC (рис.6.9) и поднимает груз F = 30 кН. Вес крана с противовесом приложен в точке О и равен по модулю G = 120 кН. Требуется определить давления колес на рельсы, когда плоскость крана параллельна линии АВ. Необходимые размеры показаны на рисунке 6.9.
Рис.6.9
Решение. Под действием вертикальных сил и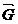 
возникают вертикальные реакции, приложенные в точках контакта колес с рельсами. В результате кран находится в равновесии под действием пяти параллельных сил: , , 
, 
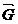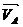и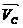 
. Для равновесия этих сил необходимо выполнить следующие три условия:
, ,
Рациональные направления осей системы координат показаны на рис.6.9. Проецируя все силы на вертикальную ось z,и составляя алгебраические суммы моментов относительно осей x и y, получаем следующие уравнения равновесия:
1) VA + VB + VC – F –G = 0;
2) – VA ∙1+ VB∙∙ 1 – F ∙3+ G ∙0,5 = 0;
3) – VC ∙1,8 + (F + G)∙0,9 = 0.
Из уравнения 3) находим VC = 75 кН. Затем решаем систему двух уравнений 1)и 2) и определяем VA = 22,5 кН., VB = 52,5 кН.
