Центр параллельных сил. Определение координат

Центра параллельных сил

Рассмотрим частный случай, когда параллельные силы приводят­ся к одной равнодействующей R.

Пусть некоторое твердое тело загружено в точках A₁, A₂, A₃ параллельными силами , ,  соответственно, которые направ­лены в одну сторону (рис.6.10). Установим величину, направление и точку приложения равнодействующей этих сил.

                                  Рис.6.10

Пользуясь правилом сложения двух параллельных сил  и , направленных в одну сторону, находим их равнодействующую , которая направлена параллельно заданным силам в ту же сторону, равна по модулю алгебраической их сумме: 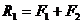    и приложе­на в точке С₁. Эта точка лежит на отрезке А₁А₂ и делит его на части, обратно пропорциональные модулям сил, т.е:

                                     A₁C₁: C₁A₂ = F₂ : F₁                                                           (6.14)

Аналогично находим равнодействующую   параллельных сил   и , т.е. равнодействующую системы трех заданных сил. Модуль равнодействующей   равен сумме модулей всех заданных сил:   

или при любом числе сил

                                                                                                                        (6.15)

Точка приложения равнодействующей к телу рас­полагается на отрезке C₁A₃ и делит этот отрезок в отношении:

CC₁: СА₃ = F₃: R₁,   или    CC₁: СА₃ = F₃: (F₁ + F₂  )                                   (6.16)

Направление равнодействующей   совпадает с направлениями задан­ных сил, а линии их действия параллельны.

Точка С, в которой приложена равнодействующая системы парал­лельных сил называется их центром. Эта точка обладает важным свой­ством, состоящим в том, что при вращении заданных сил вокруг их точек приложения без нарушения параллельности линий их действия, равнодействующая будет вращаться вокруг точки С, оставаясь па­раллельной заданным силам. На рис.6.10 показаны штриховыми линиями возможные положения заданных сил и их равнодействующей , если отклонить их на некоторый угол α от первоначального состояния. При этом положение точки С не меняется.

Для определения положения центра С параллельных сил в прост­ранстве аналитическим методом, отнесем заданные силы к системе координат с началом в точке О. При этом одну из осей координат (например, ось z) направим параллельно силам (рис.6.11).

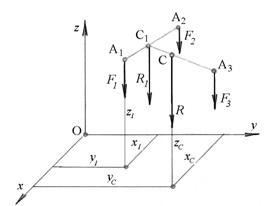
                                               Рис.6.11

Обозначим координаты точек приложения заданных сил через x, y, z с индексами соответствующими индексам заданных сил, т.е. A₁ (x₁, y₁, z₁); A₂ (x₂, y₂, z₂); A₃ (x₃, y₃, z₃), а координаты их центра через x_с, y_с, z_с.

Так как силы параллельны оси z, то легко составить алгеб­раические суммы моментов этих сил относительно осей y и x. Согласно теореме Вариньона, сумма моментов всех сил относительно произвольной оси равна моменту равнодействующей этих сил относи­тельно той же оси. Поэтому:

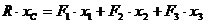                                                                         (6.17)

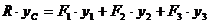                                                                        (6.18)

Если повернуть все силы и их равнодействующую так, чтобы их линии действия оказались параллельными оси y, а затем воспользо­ваться теоремой Вариньона относительно этой оси, то в результате получим:

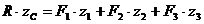                                                                          (6.19)

       Из зависимостей (6.17)-(6.19) с учетом зависимости (6.15), устанавливаем аналитические выражения для вычисления координат центра параллельных сил:

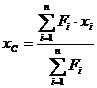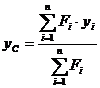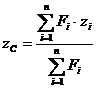                     , ,                                     (6.20)

Формулы (6.20) позволяют определить координаты центра любого чис­ла параллельных сил, приводящихся к одной равнодействующей. Если при этом заданные силы направлены в разные стороны, то они должны быть приняты с противоположными знаками. Силы, имеющие то же на­правление, что и их равнодействующая , принимаются с положительными знаками.