В предыдущих параграфах настоящей главы рассмотрены теоремы о приведении плоской системы сил к заданному центру. В результате получены векторное выражение для определения главного вектора и алгебраическое выражение для определения главного момента, т.е. выражения (4.3) и (4.4).
Покажем, что модуль, направление и линия действия равнодействующей плоской системы сил могут быть определены графическим способом, т.е. путем построения силового и веревочного многоугольников. Этот способ предложен Кульманом и называется способом "веревочного многоугольника".
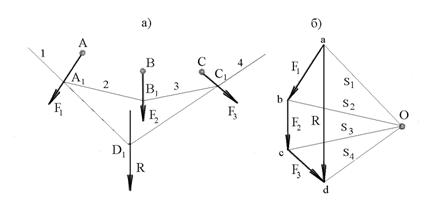
Рис.4.5
Пусть заданы три силы  ,
,  и
и  , приложенные к телу в точках А, В, С соответственно и расположенные в одной плоскости (рис.4.5,а). Найдем величину и направление равнодействующей
, приложенные к телу в точках А, В, С соответственно и расположенные в одной плоскости (рис.4.5,а). Найдем величину и направление равнодействующей  заданных сил. Для этого зададимся подходящим масштабом сил
заданных сил. Для этого зададимся подходящим масштабом сил  и построим силовой многоугольник а bcd (рис.4.5,б) в следующем порядке: из произвольной точки а плоскости действия сил откладываем отрезок а b геометрически равный силе
и построим силовой многоугольник а bcd (рис.4.5,б) в следующем порядке: из произвольной точки а плоскости действия сил откладываем отрезок а b геометрически равный силе  , из полученной точки b откладываем в том же масштабе отрезок bc геометрически равный силе
, из полученной точки b откладываем в том же масштабе отрезок bc геометрически равный силе  , затем откладываем отрезок cd геометрически равный силе
, затем откладываем отрезок cd геометрически равный силе  . Замыкающий вектор а d силового многоугольника, проведенный из начала первой силы в конец последней представляет равнодействующую
. Замыкающий вектор а d силового многоугольника, проведенный из начала первой силы в конец последней представляет равнодействующую  трех заданных сил. Модуль равнодействующей определяется измерением отрезка ad в принятом масштабе сил, т.е.
трех заданных сил. Модуль равнодействующей определяется измерением отрезка ad в принятом масштабе сил, т.е. 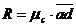 . Направление равнодействующей должно быть противоположным направлениям сторон силового многоугольника, геометрически равных заданным силам.
. Направление равнодействующей должно быть противоположным направлениям сторон силового многоугольника, геометрически равных заданным силам.
Построенный многоугольник а bcd называется планом сил и дает возможность определить величину и направление равнодействующей  .
.
Остается найти точку приложения равнодействующей. Для этого необходимо построить веревочный многоугольник. Возьмем произвольную точку О вблизи плана сил (рис.4.5,б) и соединим её с вершинами многоугольника сил а bcd. Точка О называется полюсом, а прямые О а, O b, О с, О d - лучами многоугольника сил. Обозначим их буквами 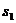 ,
, 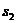 ,
, 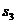 ,
, 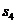 и обратим внимание на то, что каждая сторона (сила) многоугольника а bcd, включая равнодействующую
и обратим внимание на то, что каждая сторона (сила) многоугольника а bcd, включая равнодействующую  , расположена между двумя лучами (рис.4.5,б). Например, сила
, расположена между двумя лучами (рис.4.5,б). Например, сила  , заключена между лучами
, заключена между лучами 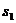 и
и 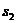 .
.
Обратимся теперь к рис.4.5,а и проведем через произвольную точку А1 взятую на линии действия силы  ,, прямые I и 2, соответственно параллельные лучам
,, прямые I и 2, соответственно параллельные лучам 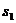 и
и 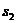 . Продолжим прямую 2 до пересечения с линией действия силы
. Продолжим прямую 2 до пересечения с линией действия силы  точке B1 и проведем из этой точки прямую 3 параллельную лучу
точке B1 и проведем из этой точки прямую 3 параллельную лучу 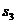 до пересечения с линией действия силы
до пересечения с линией действия силы  в точке C1. Через точку С1 проводим прямую 4 параллельную лучу
в точке C1. Через точку С1 проводим прямую 4 параллельную лучу 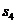 . Продолжим затем прямые I и 4 до их пересечения в точке D1. В результате получим многоугольник А1В1С1D1, называемый веревочным многоугольником. Его стороны соответственно параллельны лучам силового многоугольника (плана сил).
. Продолжим затем прямые I и 4 до их пересечения в точке D1. В результате получим многоугольник А1В1С1D1, называемый веревочным многоугольником. Его стороны соответственно параллельны лучам силового многоугольника (плана сил).
Опуская доказательство, укажем, что линия действия равнодействующей  проходит через точку D1, а её точка приложения может быть выбрана произвольно на её линии действия. Используя изложенный выше способ, можно определить равнодействующую произвольного числа сил, расположенных в одной плоскости.
проходит через точку D1, а её точка приложения может быть выбрана произвольно на её линии действия. Используя изложенный выше способ, можно определить равнодействующую произвольного числа сил, расположенных в одной плоскости.
При определении равнодействующей системы сил графическим способом может оказаться, что силовой и веревочный многоугольники замкнуты. В этом случае равнодействующая заданных сил равна нулю, т.е. заданные силы находятся в равновесии.






