Положим, что в плоскости чертежа (рис.3.8,а) действуют три пары, моменты которых соответственно равны 
, 
и 
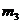. Направления их действия указаны на чертеже стрелками.
Возьмем произвольный отрезок АВ = h (рис.3.8,б) и на основании следствия б) свойства 3 эквивалентности пар приведем все заданные пары к этому отрезку h (плечу). При этом силы, образующие пары с общим плечом h будемоткладывать от точек А и В перпендикулярно отрезку АВ в направлениях, которые соответствуют направлениям действия заданных пар.
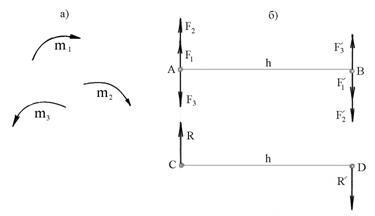
Рис.3.8
Так как пары, имеющие моменты и действуют по часовой стрелке, то силы 
и 
направляем вверх от точки А, а силы 
и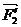 
- вниз от точки В. Силы 
и 
следует направить противоположно первым двум силам. Модули сил , и определяем из условия равенства моментов заданных пар и пар, приведенных к общему плечу АВ, т.е. из равенств:
, 
, 
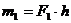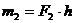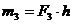
Откуда находим:
, 
, 
(3.10)
Силы , и , приложенные в точке А и действующие вдоль одной прямой приводятся к равнодействующей 
, направленной вдоль той же прямой и равной по модулю алгебраической сумме этих сил:
(3.11)
Аналогично силы , 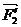и приводятся к равнодействующей 
, модуль которой определяется выражением:
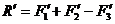(3.12)
Силы и параллельны между собой, направлены в противоположные стороны и имеют равные модули (согласно равенствам: 3.11 и 3.12).
Следовательно, эти силы образуют пару сил (, ), которая является равнодействующей заданных пар. На рис.3.8,б эта пара перемещена в положение CD.
Покажем, что момент равнодействующей пары равен алгебраической сумме моментов составляющих пар.
Обозначим момент пары (, ) буквой m, и вычислим его значение по известной формуле 
Заменив модуль равнодействующей её значением из равенства (3.11), получаем:
Приведенное доказательство теоремы является справедливым и для произвольного числа пар, т.е:
(3.13)
3.5. Условие равновесия пар.
Для равновесия твердого тела, загруженного системы пар сил, расположенных в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равной нулю.
Допустим, что под действием трех пар, показанных на рис.34,а тело находится в равновесии. После приведения заданных пар к общему плечу h (рис.3.8,б), получим три новых пары сил, две из которых действуют по часовой стрелке, а одна противоположно. Так как по условию эти пары сил находятся в равновесии, то очевидно, что
и 
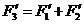
Согласно равенствам (3.11) и (3.12) имеем: 
. Следовательно, момент уравновешивающей пары равен нулю. Тогда из выражения (3.13) получим условие равновесия плоской системы пар:
(3.14)
Условие (3.14) позволяет составить уравнение равновесия плоской системы пар и определить неизвестные параметры одной из них.
