Многопролетных балок
Существуют два метода определения реакций опор однопролетной и многопролетной балок: аналитический и графический. Первый из них является основным и позволяет вычислить значения реакций опор с высокой степенью точности. Он основан на использовании условий равновесия плоской системы сил. Если при этом рационально выбрать направления осей проекций и положения моментных точек, то полученные уравнения равновесия окажутся с разделенными неизвестными, т.е. каждое из уравнений будет содержать только одну неизвестную.
Графический способ основан на использовании теории силового и веревочного многоугольников, которые являются замкнутыми для систем, находящихся в равновесии. Этот метод требует строгого соблюдения масштаба сил и параллельности линий при построении силового и веревочного многоугольников. Он широко используется в статике сооружений при расчете ферм. В остальных случаях применяется аналитический метод.
Рассмотрим несколько примеров определения реакций опор однопролетной балки на двух опорах и составной балки.
Пример 10. Балка на двух шарнирных опорах загружена равномерно распределенной нагрузкой интенсивностью q = 20 кН/м и сосредоточенной силой
F = 60 кН (рис.5.7). Требуется найти величины и направления реакций опор.

Рис.5.7
Решение. Для определения реакций опор заменим равномерно распределенную нагрузку q её равнодействующей  , приложенной в центре тяжести участка, на котором приложена эта нагрузка. Модуль равнодействующей равен произведению интенсивности нагрузки q на длину участка её распределения, т.е.
, приложенной в центре тяжести участка, на котором приложена эта нагрузка. Модуль равнодействующей равен произведению интенсивности нагрузки q на длину участка её распределения, т.е. 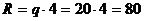 кН.
кН.
В результате балка будет загружена двумя параллельными силами  и
и  , направленными вертикально вниз. Кроме них на балку действуют реакции опор, направления которых устанавливаются в зависимости от характера этих опор. Реакция подвижной опоры
, направленными вертикально вниз. Кроме них на балку действуют реакции опор, направления которых устанавливаются в зависимости от характера этих опор. Реакция подвижной опоры  всегда направлена перпендикулярно направлению её подвижности, в данном случае вертикально вверх. Реакция неподвижной шарнирной опоры А проходит через её центр, но неизвестна по величине и направлению. В общем случае нагружения балки произвольными силами, её следует разложить на две составляющие: горизонтальную
всегда направлена перпендикулярно направлению её подвижности, в данном случае вертикально вверх. Реакция неподвижной шарнирной опоры А проходит через её центр, но неизвестна по величине и направлению. В общем случае нагружения балки произвольными силами, её следует разложить на две составляющие: горизонтальную  и вертикальную
и вертикальную  , модули которых неизвестны. Однако, в данном примере заданные силы и реакция опоры В параллельны между собою и направлены вертикально, следовательно, реакция опоры А будет иметь только вертикальную составляющую
, модули которых неизвестны. Однако, в данном примере заданные силы и реакция опоры В параллельны между собою и направлены вертикально, следовательно, реакция опоры А будет иметь только вертикальную составляющую  .
.
Для равновесия балки под действием сил, представленных на рис.5.7 необходимо выполнить следующие условия равновесия:
 и
и 
Суммируя моменты всех сил относительно опорных точек А и В, получаем следующие уравнения:
1) 
2) 
Решение этих уравнений при F = 60 кН и R = 80 кН приводит к следующему результату: V A = 75 кН, V В = 65 кН.
Положительные значения реакций  и
и  подтверждают правильность принятых направлений. Проецируя все силы на вертикальную ось y, и вычисляя их сумму, убеждаемся, что значения реакций опор вычислены правильно.
подтверждают правильность принятых направлений. Проецируя все силы на вертикальную ось y, и вычисляя их сумму, убеждаемся, что значения реакций опор вычислены правильно.
 - V A + V В – F – R =0, 75+65-60-80=0, т.е. 0=0
- V A + V В – F – R =0, 75+65-60-80=0, т.е. 0=0
Пример 11. Балка, представленная на рис.5.8, загружена произвольными силами, включая пару сил, момент которой показан стрелкой. Требуется определить реакции опор балки, если F = 40 кН m= 50 кНм.

Рис.5.8
Решение. Показываем все силы, действующие на балку: активные силы  и m и реактивные
и m и реактивные  ,
,  и
и  (рис.5.8).
(рис.5.8).
Записываем три условия равновесия системы сил, действующих на балку:
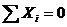 ,
,  и
и 
Составляем уравнения равновесия:
1) HА - F∙cos600=0
2) VВ∙ 5 - F∙cos3 00∙1,5 – m=0
3) - V A∙5 + F∙cos3 00∙3,5 + m=0
Подставляем заданные значения F и m в эти уравнения и вычисляем модули искомых реакций: HА= 20 кН, V В = 20,39 кН,
VA = 14,25 кН.
Аналогично определяются реакции опор балки с консолью, представленной на рис.5.9.

Рис.5.9
Предлагаем учащимся рационально выбрать условия равновесия, вычислить модули реакций опор и установить их истинные направления при q= 30 кН/м, F = 50 кН и m= 60 кНм.
Пример 12. Определить реакции опор составной балки, состоящей из двух стержней, объединенных шарниром С и загруженной силами F1 = 120 кН, F2 = 90 кН, F3 = 60 кН. Направления сил и размеры участков балки (в метрах) показаны на рис.5.10.

Рис.5.10
Решение. Кроме внешних заданных сил на балку действуют реакции опор А, В, D и шарнира С. Реакции  и
и  шарнирно подвижных опор направлены вертикально (перпендикулярно оси балки). Полагаем, что они действуют вверх. Реакцию неподвижной опоры А разложим на вертикальную
шарнирно подвижных опор направлены вертикально (перпендикулярно оси балки). Полагаем, что они действуют вверх. Реакцию неподвижной опоры А разложим на вертикальную  и горизонтальную
и горизонтальную  составляющие.
составляющие.
В точке С объединены два стержня при помощи неподвижного цилиндрического шарнира. Следовательно, в этой точке действуют по две равные и противоположно направленные силы: вертикальные  и
и  , а также горизонтальные
, а также горизонтальные 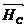 и
и  . При этом силы
. При этом силы  и
и 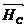 приложены к правому концу С левого стержня, а силы
приложены к правому концу С левого стержня, а силы  и
и  к левому концу С правого стержня. Для определения четырех неизвестных реакций опор (по условию не требуется определять реакции шарнира С) используем следующие четыре условия равновесия:
к левому концу С правого стержня. Для определения четырех неизвестных реакций опор (по условию не требуется определять реакции шарнира С) используем следующие четыре условия равновесия:
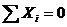 ,
,  ,
,  ,
, 
Последние два условия выражают равенство нулю суммы моментов всех сил, соответственно приложенных к правой балке CD и к левой балке АС, относительно точки С.
Составляем уравнения равновесия:
1) 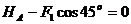 ,откуда
,откуда
 кН.
кН.
2) 
3) 
4) 
П одставляем в эти уравнения численные значений заданных сил, получаем:
- из уравнения 3 -  кН.
кН.
- из уравнения 2 -  кН.
кН.
- из уравнения 4 - 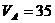 кН.
кН.
Для контроля правильности решения примера составляем сумму проекций всех сил, действующих на балку, на вертикальную ось y и приравниваем эту сумму к нулю:

 , или 0=0
, или 0=0
Примечание: Следует иметь в виду, что равные и противоположно направленные силы  и
и  , а также
, а также 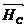 и
и  приложены к разным телам. Поэтому нельзя говорить, что они взаимно уравновешиваются. В составленных ранее уравнениях равновесия эти силы не содержатся по той причине, что сумма их моментов относительно любой точки, а также сумма проекций на любую ось равны нулю тождественно.
приложены к разным телам. Поэтому нельзя говорить, что они взаимно уравновешиваются. В составленных ранее уравнениях равновесия эти силы не содержатся по той причине, что сумма их моментов относительно любой точки, а также сумма проекций на любую ось равны нулю тождественно.




